【题目】如图,在长度为1个单位长度的小正方形组成的方格形中,点A、B、C在小正方形的顶点上.在BC上找一点P,使点P到AB和AC的距离相等.
实验与操作:
(1)在BC上找一点P,使点P到AB和AC的距离相等;
(2)在射线AP上找到一点Q,使QB=QC.
探索与计算:
如果A点坐标为(-1,-3),
(1)试在图中建立平面直角坐标系;
(2)若点M、N是坐标系中小正方形的顶点,且四边形QCMN是一个正方形,则 M点的坐标是__________,N点的坐标是___________.

参考答案:
【答案】(1)见解析;(2)(-2,-2)或(0,8),(3,-3)或(5,7).
【解析】试题分析:实验与操作:(1)P为∠BAC的平分线与BC的交点;
(2)Q为射线AP与线段BC的垂直平分线的交点;
探索与计算:(1)根据A点坐标为(-1,-3)建立直角坐标系即可;
(2)根据作出的图形,直接写出M、N的坐标即可.
试题解析:解:实验与操作:(1)如图点P (2)如图点Q;

探索与计算:(1)如图建立坐标系;(2)M(-2,-2);N(3,-3)
分两种情况讨论:
①当M、N在线段CQ的下方时,由作出的图形可知:M(-2,-2);N(3,-3);
②当M、N在线段CQ的上方时,由作出的图形可知:M(0,8);N(5,7)。
综上所述:M(-2,-2);N(3,-3)或M(0,8);N(5,7)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索练习:某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,其中成人票是每张8元,学生票是每张5元,筹得票款6950元.问成人票与学生票各售出多少张?
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定一种运算“△”满足:a△b=a2-b3,求(-5)△(-2)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(a2)3=( )
A.a6B.a5C.a3D.a﹣1
-
科目: 来源: 题型:
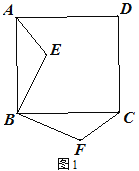
查看答案和解析>>【题目】已知正方形ABC D,E为平面内任意一点,连接AE,BE,将△ABE绕点B顺时针旋转90°得到△BFC.
(1)如图1,求证:①
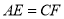 ;②
;②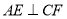 .
.(2)若
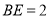 ,
,① 如图2,点E在正方形内,连接EC,若
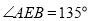 ,
, 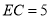 ,求
,求 的长;
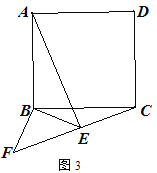
的长;② 如图3,点E在正方形外,连接EF,若AB=6,当C、E、F在一条直线时,
求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上.(每个小方格的顶点叫格点)

(1)画出△ABC向下平移3个单位后的△A1B1C1;
(2)画出△ABC绕点O顺时针旋转90°后的△A2B2C2,并求点A旋转到A2所经过的路线长.
相关试题

