【题目】如图,已知在Rt△ABC中,∠C=900,AD是∠BAC的角分线.
(1)以AB上的一点O为圆心,AD为弦在图中作出⊙O.(不写作法,保留作图痕迹);
(2)试判断直线BC与⊙O的位置关系,并证明你的结论;

参考答案:
【答案】(1)作图见解析;(2)相切;证明见解析.
【解析】试题分析(1)因为AD是弦,所以圆心O即在AB上,也在AD的垂直平分线上;
(2)因为D在圆上,所以只要能证明OD⊥BC就说明BC为⊙O的切线.
试题解析:(1)如图所示,
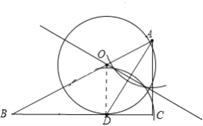
(2)相切;理由如下:
证明:连结OD,
∵OA=OD,
∴∠OAD=∠ODA
∵AD是BAC的角平分线,则∠OAD=∠DAC,
∴∠ODA=∠DAC,
∵AC⊥BC,则∠DAC+∠ADC=90°,
∴∠ODA+∠ADC=90°,即∠ODC=90°,
∴OD⊥BC,
即BC是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.内错角相等B.过一点有且只有一条直线与已知直线垂直
C.同位角相等,两直线平行D.一个角的补角大于这个角
-
科目: 来源: 题型:
查看答案和解析>>【题目】
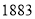 年,德国数学家格奥尔格康托尔引入位于一条线段上的一些点的集合,他的做法如下:
年,德国数学家格奥尔格康托尔引入位于一条线段上的一些点的集合,他的做法如下:取一条长度为
 的线段,将它三等分,去掉中间一段,余下两条线段,达到第
的线段,将它三等分,去掉中间一段,余下两条线段,达到第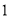 阶段;将剩下的两条线段再分别三等分.各去掉中间一段,余下四条线段,达到第
阶段;将剩下的两条线段再分别三等分.各去掉中间一段,余下四条线段,达到第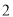 阶段;再将剩下的四条线段,分别三等分,各去掉中间一段,余下八条线段,达到第
阶段;再将剩下的四条线段,分别三等分,各去掉中间一段,余下八条线段,达到第 线段;
线段; 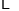 ;这样的操作一直继续下去,在不断分割舍弃的过程中,所形成的线段数目越来越多,把这种分形,称做康托尔点集.下图是康托尔点集的最初几个阶段,当达到
;这样的操作一直继续下去,在不断分割舍弃的过程中,所形成的线段数目越来越多,把这种分形,称做康托尔点集.下图是康托尔点集的最初几个阶段,当达到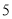 个阶段时(
个阶段时(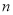 为正整数),的线段的长度之和为__________.
为正整数),的线段的长度之和为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45度.给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧AE是劣弧DE的2倍;⑤AE=BC.其中正确结论的序号是( )
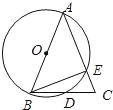
A. ①②③ B. ①②④ C. ①②⑤ D. ①②③⑤
-
科目: 来源: 题型:
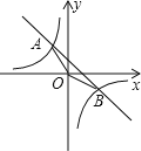
查看答案和解析>>【题目】如图,已知一次函数y=kx+b的图象与反比例函数
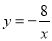 的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,求:(1)一次函数的解析式;
(2)△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
(1)求证:△ODM∽△MCN;
(2)设DM=x,OA=R,求R关于x的函数关系式;
(3)在动点O逐渐向点D运动(OA逐渐增大)的过程中,△CMN的周长如何变化?说明理由.

相关试题

