【题目】在△ABC中,AB=AC,BD=CD,∠BAD=40°,AD=AE.求∠CDE的度数. 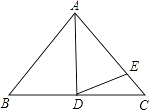
参考答案:
【答案】解:∵AB=AC,
∴△ABC为等腰三角形,
∵AD=AE,
∴△ADE为等腰三角形,
∵∠BAD=40°,
∴∠DAE=40°,
∴∠ADE= ![]() (180°﹣∠DAE)=
(180°﹣∠DAE)= ![]() (180°﹣40°)=70°,
(180°﹣40°)=70°,
又∵△ABC为等腰三角形,BD=CD,
∴AD⊥CD(三线合一),
∴∠CDE=90°﹣∠ADE=90°﹣70°=20°.
故答案为:20°
【解析】首先得到△ABC,△ADE均为等腰三角形,再根据等腰三角形的性质求解.
【考点精析】通过灵活运用三角形的内角和外角,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】材料:一般地,n个相同因数a相乘:记为an . 如23=8,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么(log216)2+
 log381= .
log381= . -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由.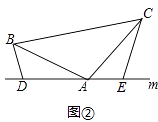
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题。
(1)求出下列各数:①25的平方根; ②﹣27的立方根; ③ 的相反数.
的相反数.
(2)将(1)中求出的每个数准确地表示在数轴上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B坐标分别为(4,0)、(0,8),点C是线段OB上一动点,点E在x轴正半轴上,四边形OEDC是矩形,且OE=2OC.设OE=t(t>0),矩形OEDC与△AOB重合部分的面积为S.根据上述条件,回答下列问题:
(1)当矩形OEDC的顶点D在直线AB上时,t= ;
(2)当t=4时,直接写出S的值;
(3)求出S与t的函数关系式;
(4)若S=12,则t= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】全面贯彻落实“大气十条”,抓好大气污染防治,是今年环保工作的重中之重.其中推进燃煤电厂脱硫改造15000 000千瓦是《政府工作报告》中确定的重点任务之一.将数据15 000 000用科学记数法表示为( )
A.15×106
B.1.5×107
C.1.5×108
D.0.15×108 -
科目: 来源: 题型:
查看答案和解析>>【题目】要调查下列问题,你认为哪些适合抽样调查:①了解全国手机用户对废手机的处理情况;②检测某地区空气的质量;③调查全市中学生一天的学习时间( )
A. ①② B. ①③ C. ②③ D. ①②③
相关试题

