【题目】如图,点A、B坐标分别为(4,0)、(0,8),点C是线段OB上一动点,点E在x轴正半轴上,四边形OEDC是矩形,且OE=2OC.设OE=t(t>0),矩形OEDC与△AOB重合部分的面积为S.根据上述条件,回答下列问题:
(1)当矩形OEDC的顶点D在直线AB上时,t= ;
(2)当t=4时,直接写出S的值;
(3)求出S与t的函数关系式;
(4)若S=12,则t= .

参考答案:
【答案】(1)t=![]() (2) 7(3)
(2) 7(3) (4)8
(4)8
【解析】试题分析:(1)证明△BCD∽△BOA,利用线段比求出t值.(2)当t=4时,点E与A重合,证明△CBF∽△OBA求出CF.(3)根据t的取值范围求出S的值.(4) 由题意可知把S=12代入S=![]()
![]() t2+2t中,
t2+2t中, ![]()
![]() t2+2t=12,整理,得t2-32t+192=0.解得 t1=8,t2=24>16(舍去)
t2+2t=12,整理,得t2-32t+192=0.解得 t1=8,t2=24>16(舍去)![]() 当S=12时,t=8.
当S=12时,t=8.
试题解析:
(1)由题意可得∠BCD=∠BOA=90°,∠CBD=∠OBA,
∴△BCD∽△BOA,
∴![]()
而CD=OE=t,BC=8CO=8![]() ,OA=4,
,OA=4,
则8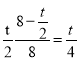 ,解得t=
,解得t=![]() ,
,
∴当点D在直线AB上时,t=![]() .
.
(2)(2)当t=4时,点E与A重合,设CD与AB交于点F,
则由△CBF∽△OBA得![]() ,
,
即![]() ,解得CF=3,
,解得CF=3,
∴S=![]() OC(OE+CF)=
OC(OE+CF)=![]() ×2×(3+4)=7.
×2×(3+4)=7.
(3)![]() 当0<t≤
当0<t≤![]() 时,S=
时,S=![]() t2,
t2,
![]() 当
当![]() <t≤4时,如图(2),
<t≤4时,如图(2),

∵A(4,0),B(0,8)
∴直线AB的解析式为y=-2x+8,G(t, ![]() 2t+8),F(4
2t+8),F(4![]()
![]() ,
,![]() ),
),
∴DF=![]()
![]() 4,DG=
4,DG=![]()
![]() 8,
8,
∴S=S矩形COED-S△DFG=t×![]()
![]()
![]() (
(![]()
4)( ![]()
![]() 8)
8)
=-![]() t2+10t-16.
t2+10t-16.

![]() 当
当![]() 时,如图(3)
时,如图(3)
由∠BFC=∠BAO tan∠BAO=tan∠BFC
![]() =2
=2 ![]()
∴S=S△BOA![]() S△BCF=
S△BCF=![]() ×4×8
×4×8![]()
![]() ×(4
×(4![]() -
-![]() )(8
)(8![]()
![]() =
=![]()
![]() t2+2t.
t2+2t.
综上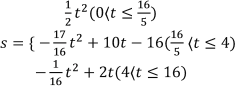 (4)8
(4)8
(提示:由题意可知把S=12代入S=![]()
![]() t2+2t中,
t2+2t中, ![]()
![]() . t2+2t=12,整理,得t2-32t+192=0.解得 t1=8,t2=24>16(舍去)
. t2+2t=12,整理,得t2-32t+192=0.解得 t1=8,t2=24>16(舍去)![]() 当S=12时,t=8.)
当S=12时,t=8.)
点睛: 本题考查的是二次函数的综合运用,相似三角形的判定以及考生的做题能力,解题时要注意分段函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由.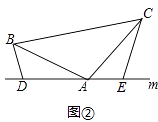
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题。
(1)求出下列各数:①25的平方根; ②﹣27的立方根; ③ 的相反数.
的相反数.
(2)将(1)中求出的每个数准确地表示在数轴上.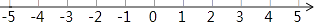
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,BD=CD,∠BAD=40°,AD=AE.求∠CDE的度数.
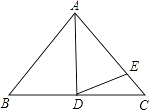
-
科目: 来源: 题型:
查看答案和解析>>【题目】全面贯彻落实“大气十条”,抓好大气污染防治,是今年环保工作的重中之重.其中推进燃煤电厂脱硫改造15000 000千瓦是《政府工作报告》中确定的重点任务之一.将数据15 000 000用科学记数法表示为( )
A.15×106
B.1.5×107
C.1.5×108
D.0.15×108 -
科目: 来源: 题型:
查看答案和解析>>【题目】要调查下列问题,你认为哪些适合抽样调查:①了解全国手机用户对废手机的处理情况;②检测某地区空气的质量;③调查全市中学生一天的学习时间( )
A. ①② B. ①③ C. ②③ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况:

(1)将下面的表格补充完整:
(2)根据规律,是否存在一个正多边形,其中的∠α=21°?若存在,请求出n的值,若不存在,请说明理由.正多边形边数
3
4
5
6
…
n
∠α的度数
60°
…
相关试题

