【题目】如图, ![]() 是
是 ![]() 的直径,
的直径, ![]() 是弦,
是弦, ![]() ,
, ![]() .若用扇形
.若用扇形 ![]() (图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是 .
(图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是 . 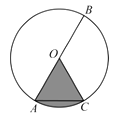
参考答案:
【答案】![]()
【解析】解:因为∠BOC=2∠AOC,∠BOC+∠AOC=180°,
所以3∠AOC=180°,
解得∠AOC=60°,
又因为OA=OC,
所以△AOC是等边三角形
即AO=AC=3,
则弧AC的长为![]()
则圆锥底面的半径为![]()
所以答案是![]()
【考点精析】解答此题的关键在于理解弧长计算公式的相关知识,掌握若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的,以及对圆锥的相关计算的理解,了解圆锥侧面展开图是一个扇形,这个扇形的半径称为圆锥的母线;圆锥侧面积S=πrl;V圆锥=1/3πR2h..
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
(1)如图1,在半对角四边形ABCD中,∠B= ∠D,∠C=
∠D,∠C=  ∠A,求∠B与∠C的度数之和;
∠A,求∠B与∠C的度数之和;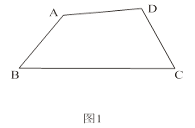
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO.∠OBA的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.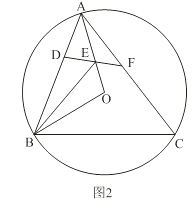
求证:四边形DBCF是半对角四边形;
(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G.当DH=BG时,求△BGH与△ABC的面积之比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,
,  .以
.以  为直径的
为直径的  交
交  于点
于点  ,
,  是
是  上一点,且
上一点,且 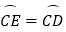 ,连接
,连接 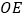 ,过点
,过点  作
作 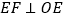 ,交
,交  的延长线于点
的延长线于点 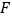 ,则
,则  的度数为( )
的度数为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
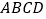 中,
中, 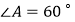 ,
, 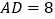 ,
, 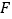 是
是  的中点.过点
的中点.过点 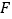 作
作 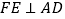 ,垂足为
,垂足为 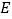 .将
.将 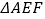 沿点
沿点 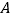 到点
到点 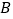 的方向平移,得到
的方向平移,得到  .设
.设 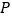 、
、 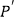 分别是
分别是 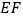 、
、 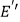 的中点,当点
的中点,当点 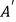 与点
与点 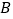 重合时,四边形
重合时,四边形 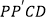 的面积为( )
的面积为( )
A.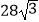
B.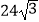
C.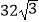
D.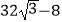
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一笔直的沿湖道路
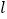 上有
上有  、
、 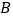 两个游船码头,观光岛屿
两个游船码头,观光岛屿 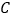 在码头
在码头  北偏东
北偏东 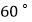 的方向,在码头
的方向,在码头 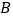 北偏西
北偏西  的方向,
的方向, 
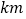 .游客小张准备从观光岛屿
.游客小张准备从观光岛屿 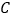 乘船沿
乘船沿  回到码头
回到码头  或沿
或沿  回到码头
回到码头 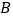 ,设开往码头
,设开往码头  、
、 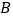 的游船速度分别为
的游船速度分别为 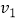 、
、  ,若回到
,若回到  、
、  所用时间相等,则
所用时间相等,则  (结果保留根号).
(结果保留根号).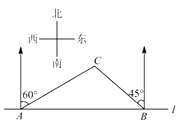
-
科目: 来源: 题型:
查看答案和解析>>【题目】某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费
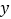 (元)是行李质量
(元)是行李质量 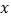 (
( 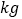 )的一次函数.已知行李质量为
)的一次函数.已知行李质量为 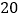
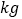 时需付行李费
时需付行李费 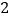 元,行李质量为
元,行李质量为 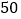
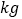 时需付行李费
时需付行李费 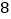 元.
元.
(1)当行李的质量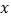 超过规定时,求
超过规定时,求 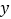 与
与 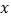 之间的函数表达式;
之间的函数表达式;
(2)求旅客最多可免费携带行李的质量. -
科目: 来源: 题型:
查看答案和解析>>【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
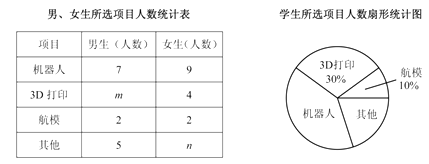
根据以上信息解决下列问题:
(1)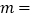 ,
, 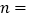 ;
;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ;
;
(3)从选航模项目的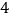 名学生中随机选取
名学生中随机选取 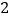 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的 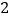 名学生中恰好有
名学生中恰好有 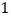 名男生、
名男生、 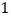 名女生的概率.
名女生的概率.
相关试题

