【题目】如图,已知一次函数的图象y=kx+b与反比例函数y=﹣ ![]() 的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,求:
的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,求: 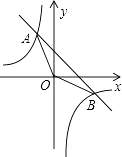
(1)一次函数的解析式;
(2)△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
参考答案:
【答案】
(1)解:令反比例函数y=﹣ ![]() 中x=﹣2,则y=4,
中x=﹣2,则y=4,
∴点A的坐标为(﹣2,4);
反比例函数y=﹣ ![]() 中y=﹣2,则﹣2=﹣
中y=﹣2,则﹣2=﹣ ![]() ,解得:x=4,
,解得:x=4,
∴点B的坐标为(4,﹣2).
∵一次函数过A、B两点,
∴ ![]() ,解得:
,解得: ![]() ,
,
∴一次函数的解析式为y=﹣x+2
(2)解:设直线AB与y轴交于C,
令为y=﹣x+2中x=0,则y=2,
∴点C的坐标为(0,2),
∴S△AOB= ![]() OC(xB﹣xA)=
OC(xB﹣xA)= ![]() ×2×[4﹣(﹣2)]=6
×2×[4﹣(﹣2)]=6
(3)解:观察函数图象发现:
当x<﹣2或0<x<4时,一次函数图象在反比例函数图象上方,
∴一次函数的函数值大于反比例函数的函数值时x的取值范围为x<﹣2或0<x<4
【解析】(1)由点A、B的横纵坐标结合反比例函数解析式即可得出点A、B的坐标,再由点A、B的坐标利用待定系数法即可得出直线AB的解析式;(2)设直线AB与y轴交于C,找出点C的坐标,利用三角形的面积公式结合A、B点的横坐标即可得出结论;(3)观察函数图象,根据图象的上下关系即可找出不等式的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知数轴上两点A,B对应的数分别是﹣1,3,点P为数轴上的一动点,其对应的数为x

(1)A、B两点的距离AB= ;
(2)在数轴上是否存在点P,使PA+PB=6?若存在,请求出x的值;若不存在,请说明理由.
(3)如图2,若点P以每秒1个单位的速度从点O出发向右运动,同时点A以每秒5个单位的速度向左运动,点B以每秒20个单位的速度向右运动,在运动的过程中,M、N分别是AP、OB的中点,问:
 的值是否发生变化?请说明理由.
的值是否发生变化?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】张家界市为了治理城市污水,需要铺设一段全长为300米的污水排放管道,铺设120米后,为了尽可能减少施工对城市交通所造成的影响,后来每天的工作量比原计划增加20%,结果共用了27天完成了这一任务,求原计划每天铺设管道多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,CA=CB=2,CD⊥AB于D,点P是线段CD上的一个动点,以点P为直角顶点向下作等腰直角△PBE,
连接DE ,则DE的最小值为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
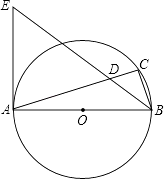
(1)∠ACB=°,理由是:;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD. -
科目: 来源: 题型:
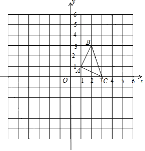
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0).(1)画出△ABC绕点O逆时针旋转90°后得到的△DEF;
(2)以点O为位似中心,在第三象限内把△ABC按相似比2:1放大(即所画△PQR与△ABC的相似比为2:1).
(3)在(2)的条件下,若M(a,b)为△ABC边上的任意一点,则△PQR的边上与点M对应的点M′的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
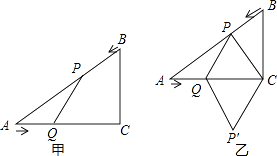
(1)设△APQ的面积为S,当t为何值时,S取得最大值?S的最大值是多少?
(2)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值;′
(3)当t为何值时,△APQ是等腰三角形?
相关试题

