【题目】如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题: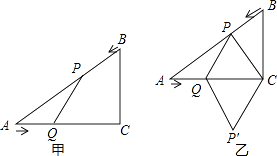
(1)设△APQ的面积为S,当t为何值时,S取得最大值?S的最大值是多少?
(2)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值;′
(3)当t为何值时,△APQ是等腰三角形?
参考答案:
【答案】
(1)
解:如图甲,过点P作PH⊥AC于H,
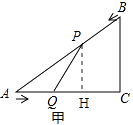
∵∠C=90°,
∴AC⊥BC,
∴PH∥BC,
∴△APH∽△ABC,
∴ ![]() ,
,
∵AC=4cm,BC=3cm,
∴AB=5cm,
∴ ![]() =
= ![]() ,
,
∴PH=3﹣ ![]() t,
t,
∴△AQP的面积为:
S= ![]() ×AQ×PH=
×AQ×PH= ![]() ×t×(3﹣
×t×(3﹣ ![]() t)=﹣
t)=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
∴当t为 ![]() 秒时,S最大值为
秒时,S最大值为 ![]() cm2
cm2
(2)
解:如图乙,连接PP′,PP′交QC于E,

当四边形PQP′C为菱形时,PE垂直平分QC,即PE⊥AC,QE=EC,
∴△APE∽△ABC,
∴ ![]() =
= ![]() ,
,
∴AE= ![]() =
= ![]() =﹣
=﹣ ![]() t+4
t+4
QE=AE﹣AQ═﹣ ![]() t+4﹣t=﹣
t+4﹣t=﹣ ![]() t+4,
t+4,
QE= ![]() QC=
QC= ![]() (4﹣t)=﹣
(4﹣t)=﹣ ![]() t+2,
t+2,
∴﹣ ![]() t+4=﹣
t+4=﹣ ![]() t+2,
t+2,
解得:t= ![]() ,
,
∵0< ![]() <4,
<4,
∴当四边形PQP′C为菱形时,t的值是 ![]() s
s
(3)
解:由(1)知,
PE=﹣ ![]() t+3,与(2)同理得:QE=AE﹣AQ=﹣
t+3,与(2)同理得:QE=AE﹣AQ=﹣ ![]() t+4
t+4
∴PQ= ![]() =
= ![]() =
= ![]() ,
,
在△APQ中,
① 当AQ=AP,即t=5﹣t时,解得:t1= ![]() ;
;
②当PQ=AQ,即 ![]() =t时,解得:t2=
=t时,解得:t2= ![]() ,t3=5;
,t3=5;
③当PQ=AP,即 ![]() =5﹣t时,解得:t4=0,t5=
=5﹣t时,解得:t4=0,t5= ![]() ;
;
∵0<t<4,
∴t3=5,t4=0不合题意,舍去,
∴当t为 ![]() s或
s或 ![]() s或
s或 ![]() s时,△APQ是等腰三角形
s时,△APQ是等腰三角形
【解析】(1)过点P作PH⊥AC于H,由△APH∽△ABC,得出 ![]() =
= ![]() ,从而求出AB,再根据
,从而求出AB,再根据 ![]() =
= ![]() ,得出PH=3﹣
,得出PH=3﹣ ![]() t,则△AQP的面积为:
t,则△AQP的面积为: ![]() AQPH=
AQPH= ![]() t(3﹣
t(3﹣ ![]() t),最后进行整理即可得出答案;(2)连接PP′交QC于E,当四边形PQP′C为菱形时,得出△APE∽△ABC,
t),最后进行整理即可得出答案;(2)连接PP′交QC于E,当四边形PQP′C为菱形时,得出△APE∽△ABC, ![]() =
= ![]() ,求出AE=﹣
,求出AE=﹣ ![]() t+4,再根据QE=AE﹣AQ,QE=
t+4,再根据QE=AE﹣AQ,QE= ![]() QC得出﹣
QC得出﹣ ![]() t+4=﹣
t+4=﹣ ![]() t+2,再求t即可;(3)由(1)知,PE=﹣
t+2,再求t即可;(3)由(1)知,PE=﹣ ![]() t+3,与(2)同理得:QE=﹣
t+3,与(2)同理得:QE=﹣ ![]() t+4,从而求出PQ=
t+4,从而求出PQ= ![]() ,
,
在△APQ中,分三种情况讨论:①当AQ=AP,即t=5﹣t,②当PQ=AQ,即 ![]() =t,③当PQ=AP,即
=t,③当PQ=AP,即 ![]() =5﹣t,再分别计算即可.
=5﹣t,再分别计算即可.
【考点精析】本题主要考查了相似三角形的应用的相关知识点,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数的图象y=kx+b与反比例函数y=﹣
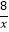 的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,求:
的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,求: 
(1)一次函数的解析式;
(2)△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
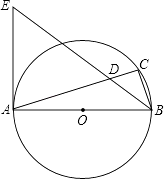
(1)∠ACB=°,理由是:;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0).(1)画出△ABC绕点O逆时针旋转90°后得到的△DEF;
(2)以点O为位似中心,在第三象限内把△ABC按相似比2:1放大(即所画△PQR与△ABC的相似比为2:1).
(3)在(2)的条件下,若M(a,b)为△ABC边上的任意一点,则△PQR的边上与点M对应的点M′的坐标为 .
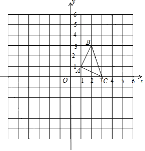
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5
B.6
C.7
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A,B是数轴上的点,请参照图并思考,完成下列各题.

(1) 若点A表示数
 ,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.
,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.(2) 若点A表示数3,将A点向左移动6个单位长度,再向右移动5个单位长度后到达点B,则B表示的数是________;此时 A,B两点间的距离是________.
(3)若A点表示的数为m,将A点向右移动n个单位长度,再向左移动t个单位长度后到达终点B,此时A、B两点间的距离为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应“学雷锋、树新风、做文明中学生”号召,某校开展了志愿者服务活动,活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项,活动期间,随机抽取了部分学生对志愿者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图.

(1)被随机抽取的学生共有多少名?
(2)在扇形统计图中,求活动数为3项的学生所对应的扇形圆心角的度数,并补全折线统计图;
(3)该校共有学生2000人,估计其中参与了4项或5项活动的学生共有多少人?
相关试题

