【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下的定义:若⊙C上存在两个点A、B,使得∠APB=60°,则称P为⊙C的可视点.
(1)当⊙O的半径为1时,
①在点![]() 、E(1,1)、F(3,0)中,⊙O的可视点是______.
、E(1,1)、F(3,0)中,⊙O的可视点是______.
②过点M(4,0)作直线l:y=kx+b,若直线l上存在⊙O的可视点,求b的取值范围;
(2)若T(t,0),⊙T的半径为1,直线y=![]() 上存在⊙T的可视点,且所有可视点构成的线段长度为n,若
上存在⊙T的可视点,且所有可视点构成的线段长度为n,若![]() ,直接写出t 的取值范围.
,直接写出t 的取值范围.
参考答案:
【答案】(1)①D、E,②![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)①根据题意举例说明即可;
②当直线l与半径为2的⊙O相切时,利用sin∠AMO=![]() ,可求得∠AMO=30°,进而可求得OE长,从而可得b的取值范围;
,可求得∠AMO=30°,进而可求得OE长,从而可得b的取值范围;
(2)当t>0时,先求直线y=![]() 与半径为2的⊙T相切时的t的值,再求直线y=
与半径为2的⊙T相切时的t的值,再求直线y=![]() 与半径为2的⊙T相交且所截线段长为
与半径为2的⊙T相交且所截线段长为![]() 时的t的值,进而求得t的取值范围.
时的t的值,进而求得t的取值范围.
解:(1)①如图,过点D作DA∥x轴,DB∥y轴,可得∠ADB=90°,当点A、B在圆上越来越靠近时,∠ADB可以为60°,则点D是可视点;
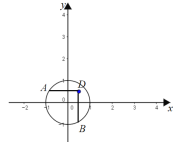
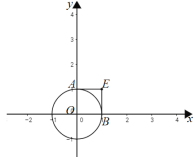
如图,过点E作⊙O的切线EA、EB,则∠OAE=∠OBE =90°
又∵∠AOB=90°,∴∠E=90°,
当点A、B在圆上越来越靠近时,∠AEB可以为60°,则点E是可视点;
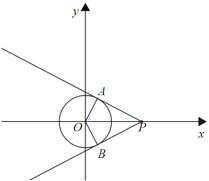
由题意可知,当点P在⊙O外时,过点P作⊙O的切线PA、PB,则此时∠APB最大,若∠APB≥60°,则⊙O上一定存在两个点A、B,使得∠APB=60°.
如图,过点P作⊙O的切线PA、PB,当∠APB=60°时,则∠APO=∠BPO=30°,
在Rt△AOP中,sin∠APO=![]() ,
,
∵OA=1,
∴OP=2
∴当OP≤2时,⊙O一定有可视点,当OP>2时,⊙O没有可视点.
∵点F(3,0),
∴OF=3>2,
∴点F不是可视点
故答案为:D、E.
②由①得,若直线l上存在⊙O的可视点,则直线l与半径为2的⊙O相切或相交;
如图,当直线l与半径为2的⊙O相切时,
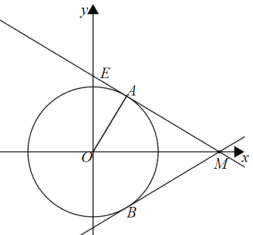
∵M(4,0),
∴OM=4,
∴在Rt△AOM中,sin∠AMO=![]() ,
,
∴∠AMO=30°,
∴在Rt△EOM中,tan∠EMO=![]() ,
,
∴![]() ,
,
∴若直线l上存在⊙O的可视点,求b的取值范围为![]() ;
;
(2)当y=0时,![]() =0,
=0,
解得,x=![]() ,则直线l与x轴的交点坐标为(
,则直线l与x轴的交点坐标为(![]() ,0),
,0),
当x=0时,y=![]() ,则直线l与y轴的交点坐标为(0,
,则直线l与y轴的交点坐标为(0,![]() ),
),
∵直线y=![]() 上存在⊙T的可视点,且⊙T的半径为1,
上存在⊙T的可视点,且⊙T的半径为1,
∴直线y=![]() 与半径为2的⊙T相交或相切
与半径为2的⊙T相交或相切
当t>0时,
如图,当直线y=![]() 与半径为2的⊙T相切时,
与半径为2的⊙T相切时,
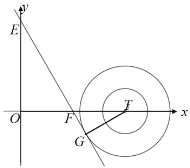
∵E(0,![]() ),F(
),F(![]() ,0),
,0),
∴OE=![]() ,OF=
,OF=![]() ,
,
∴在Rt△EOF中,tan∠EFO= ,
,
∴∠TFG=∠EFO=60°,
∵T(t,0),
∴TF=![]() ,
,
∴在Rt△TGF中,sin∠TFG=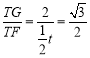 ,
,
∴![]() ,
,
如图,当直线y=![]() 与半径为2的⊙T相交且CD=
与半径为2的⊙T相交且CD=![]() 时,
时,
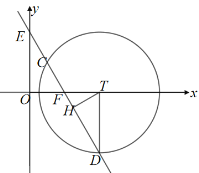
过点T作TH⊥CD,则![]()
在Rt△THD中,cos∠TDH=![]() ,
,
∴∠TDH=30°,
又∵∠TFD=60°,
∴∠DTF=90°,
∴在Rt△TFD中,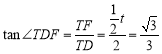 ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
同理,当t<0时,![]()
综上所述,t的取值范围为:![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在研究反比例函数
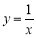 的图象与性质时,我们对函数解析式进行了深入分析.
的图象与性质时,我们对函数解析式进行了深入分析.首先,确定自变量
 的取值范围是全体非零实数,因此函数图象会被
的取值范围是全体非零实数,因此函数图象会被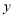 轴分成两部分;其次,分析解析式,得到
轴分成两部分;其次,分析解析式,得到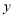 随
随 的变化趋势:当
的变化趋势:当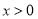 时,随着
时,随着 值的增大,
值的增大,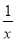 的值减小,且逐渐接近于零,随着
的值减小,且逐渐接近于零,随着 值的减小,
值的减小,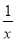 的值会越来越大…,由此,可以大致画出
的值会越来越大…,由此,可以大致画出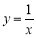 在
在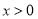 时的部分图象,如图所示:
时的部分图象,如图所示: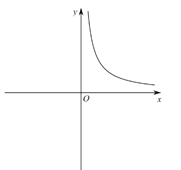
利用同样的方法,我们可以研究函数
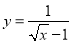 的图象与性质.通过分析解析式画出部分函数图象如图所示.
的图象与性质.通过分析解析式画出部分函数图象如图所示.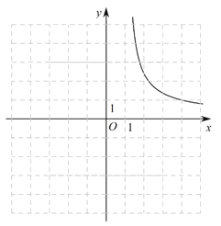
(1)请沿此思路在图中完善函数图象的草图并标出此函数图象上横坐标为0的点
 ;(画出网格区域内的部分即可)
;(画出网格区域内的部分即可)(2)观察图象,写出该函数的一条性质:__________;
(3)若关于
 的方程
的方程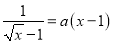 有两个不相等的实数根,结合图象,直接写出实数
有两个不相等的实数根,结合图象,直接写出实数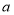 的取值范围: __________.
的取值范围: __________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=ax22a2x(a
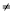 0)的对称轴与x轴交于点P.
0)的对称轴与x轴交于点P.(1)求点P的坐标(用含a的代数式表示);
(2)记函数y=x+2(1
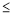 x
x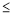 2)的图象为图形M,若抛物线与图形M恰有一个公共点,结合函数的图象,求a的取值范围.
2)的图象为图形M,若抛物线与图形M恰有一个公共点,结合函数的图象,求a的取值范围. -
科目: 来源: 题型:
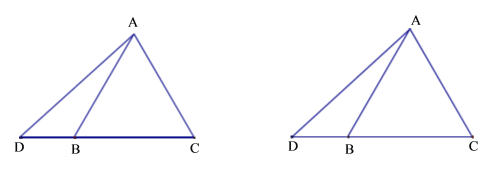
查看答案和解析>>【题目】如图,在等边△ABC中,点D 是边CB延长线上一动点(BD<BC),连接AD,点B 关于直线AD的对称点为E,过D 作DF//AB交CE于点F.
(1)依题意补全图形;
(2)求证:AD=CF;
(3)当∠DCE=15°时,直接写出线段AD,EF,BC之间的数量关系.
-
科目: 来源: 题型:
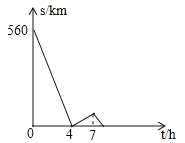
查看答案和解析>>【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,下列说法:
①甲、乙两地之间的距离为560km;
②快车速度是慢车速度的1.5倍;
③快车到达甲地时,慢车距离甲地60km;
④相遇时,快车距甲地320km;
其中正确的个数是( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
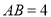 ,射线
,射线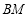 和
和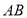 互相垂直,点
互相垂直,点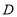 是
是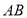 上的一个动点,点
上的一个动点,点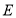 在射线
在射线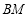 上,
上,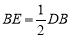 ,作
,作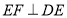 并截取
并截取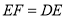 ,连结
,连结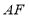 并延长交射线
并延长交射线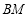 于点
于点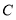 .设
.设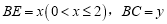 ,则
,则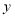 关于
关于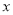 的函数解析式是( )
的函数解析式是( )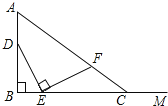
A.
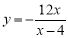 B.
B.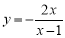 C.
C.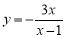 D.
D.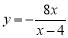
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示为二次函数
 的图象,在下列结论
的图象,在下列结论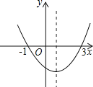
①
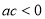 ;
;②
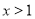 时,
时,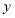 随
随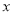 的增大而增大;
的增大而增大;③
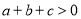 ;
;④方程
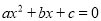 的根是
的根是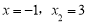 ;
;中正确的个数有( )个.
A.1B.2C.3D.4
相关试题

