【题目】已知,如图正方形ABCD中,E为BC上任意一点,过E作EF⊥BC,交BD于F,G为DF的中点,连AE和AG.
(1)如图1,求证:∠FEA+∠DAG=45°; 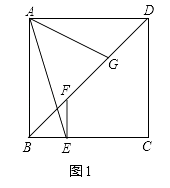
(2)如图2在(1)的条件下,设BD和AE的交点为H,BG=8,DH=9,求AD的长. 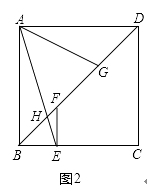
参考答案:
【答案】
(1)证明:作GM⊥BC于M,连接GE、GC,如图1,
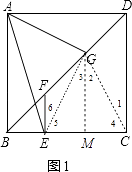
∵四边形ABCD为正方形,
∴DA=DC,∠ADB=∠CDB=45°,
在△ADG和△CDG中
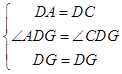 ,
,
∴△ADG≌△CDG,
∴AG=CG,∠DAG=∠1,∠AGD=∠CGD,
∵G点为DF的中点,FE⊥BC,GM⊥BC,DC⊥BC,
∴GM为梯形CDFE的中位线,
∴EM=CM,
∴GE=GC,∠5=∠4,
∴GM平分∠EGC,
∴∠2=∠3,
∴∠1=∠6=∠DAG,GA=GE,
∵GM∥CD,
∴∠MGD=180°﹣∠GDC=135°,即∠2+∠DGC=135°,
∴∠AGD+∠3=∠2+∠DGC=135°,
∴∠AGE=90°,
∴△AGE为等腰直角三角形,
∴∠AEG=45°,即∠FEA+∠6=45°,
∴∠FEA+∠DAG=45°;
(2)解:把△ADG绕点A顺时针旋转90°得到△ABQ,连接QH,如图2,
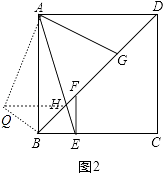
∴∠ABQ=∠ABD=45°,AQ=AD,BQ=DG,∠QAG=90°,
∵∠FEA+∠DAG=45°;
而∠FEA=∠BAE,
∴∠BAE+∠DAG=45°;
∴∠EAG=45°,
∴∠QAE=45°,
在△QAH和△GAH中
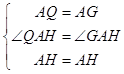 ,
,
∴△QAH≌△GAH,
∴HQ=HG,
设BH=x,则HG=BG﹣BH=8﹣x,
∴HQ=8﹣x,
∵DH=BG+DG﹣BH,
∴DG=9﹣8+x=x+1,
∴BQ=x+1,
∵∠ABQ+∠ABD=45°+45°=90°,
∴△BQH为直角三角形,
∴BQ2+BH2=QH2,即(x+1)2+x2=(8﹣x)2,解得x=3,
∴BD=BH+DH=3+9=12,
∴AD= ![]() BD=6
BD=6 ![]() .
.
【解析】(1)作GM⊥BC于M,连接GE、GC,如图1,由正方形的性质得DA=DC,∠ADB=∠CDB=45°,再证明△ADG≌△CDG得到AG=CG,∠DAG=∠1,∠AGD=∠CGD,接着利用等腰三角形的判定与性质得到GC=GE,∠5=∠4,∠2=∠3,从而得到∠1=∠6=∠DAG,GA=GE,再证明△AGE为等腰直角三角形得到∠AEG=45°,从而得到∠FEA+∠DAG=45°;(2)把△ADG绕点A顺时针旋转90°得到△ABQ,连接QH,如图2,利用旋转的性质得∠ABQ=∠ABD=45°,AQ=AD,BQ=DG,∠QAG=90°,再证明△QAH≌△GAH得到HQ=HG,设BH=x,用x表示出则HG=HQ=8﹣x,BQ=x+1,然后在Rt△BQH中利用勾股定理得到(x+1)2+x2=(8﹣x)2,解得x=3,则BD=BH+DH=12,然后根据等腰直角三角形的性质求AD.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】若a<b,下列不等式中错误的是( )
A.a+z<b+zB.a﹣c>b﹣cC.2a<2bD.﹣4a>﹣4b
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着社会的发展,私家车变得越来越普及,使用节能低油耗汽车,对环保有着非常积极的意义,某市有关部门对本市的某一型号的若干辆汽车,进行了一项油耗抽样实验:即在同一条件下,被抽样的该型号汽车,在油耗1L的情况下,所行驶的路程(单位:km)进行统计分析,结果如图所示:

(注:记A为12~12.5,B为12.5~13,C为13~13.5,D为13.5~14,E为14~14.5)
请依据统计结果回答以下问题:
(1)试求进行该试验的车辆数;
(2)请补全频数分布直方图;
(3)若该市有这种型号的汽车约900辆(不考虑其他因素),请利用上述统计数据初步预测,该市约有多少辆该型号的汽车,在耗油1L的情况下可以行驶13km以上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=kx+b(k<0)与函数
 (x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a,
(x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a, )、(c,
)、(c, ),其中a>c>0.
),其中a>c>0.(1)如图①,求证:∠EDP=∠ACP;
(2)如图②,若A、D、E、C四点在同一圆上,求k的值;
(3)如图③,已知c=1,且点P在直线BF上,试问:在线段AT上是否存在点M,使得OM⊥AM?请求出点M的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学对数据26,36,46,5□,52进行统计分析,发现其中一个两位数的个位数字被黑水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.平均数B.中位数C.方差D.极差
相关试题

