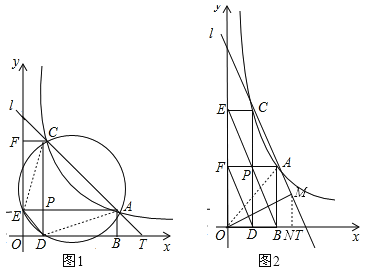
【题目】如图,直线l:y=kx+b(k<0)与函数![]() (x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a,
(x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a,![]() )、(c,
)、(c,![]() ),其中a>c>0.
),其中a>c>0.
(1)如图①,求证:∠EDP=∠ACP;
(2)如图②,若A、D、E、C四点在同一圆上,求k的值;
(3)如图③,已知c=1,且点P在直线BF上,试问:在线段AT上是否存在点M,使得OM⊥AM?请求出点M的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)证明见解析;(2)-1;(3)(![]() ,
,![]() ).
).
【解析】
试题分析:(1)由P、E、D的坐标可表示出PA、EP、PC和DP的长,可证明△EPD∽△CPA,利用相似三角形的性质可证得结论;
(2)连接AD、EC,可证明△AEC≌△CDA,可得CD=AE,把A、C坐标代入直线l解析式,可求得k的值;
(3)假设在线段AT上存在点M,使得OM⊥AM,连接OM、OA,可表示出C、F、P、B的坐标,利用直线BF的解析式可求得a的值,可求得A点坐标,可求得T点坐标,在△OAT中,利用等积法可求得OM的长,在RtOMT中可求得MT的长,作MN⊥x轴,同理可求得MN的长,则可求得ON的长,可判断N在线段BT上,满足条件,从而可知存在满足条件的M点.
试题解析:(1)证明:
由题意可知P(c,![]() ),E(0,
),E(0,![]() ),D(c,0),∴PA=a﹣c,EP=c,PC=
),D(c,0),∴PA=a﹣c,EP=c,PC=![]() ﹣
﹣![]() =
=![]() ,DP=
,DP=![]() ,∴
,∴![]() ,且∠EPD=∠APC,∴△EPD∽△CPA,∴∠EDP=∠ACP;
,且∠EPD=∠APC,∴△EPD∽△CPA,∴∠EDP=∠ACP;
(2)解:如图1,连接AD、EC,由(1)可知DE∥AC,∴∠DEC+∠ECA=180°,∵A、D、E、C四点在同圆周上,∴∠DEC+∠DAC=180°,∴∠ECA=∠DAC,在△AEC和△CDA中,∵∠ECA=∠DAC,∠AEC=∠CDA,AC=CA,∴△AEC≌△CDA(AAS),∴CD=AE,即a=![]() ,可得ac=4,∵A、C在直线l上,∴
,可得ac=4,∵A、C在直线l上,∴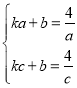 ,解得k=
,解得k=![]() =﹣
=﹣![]() =﹣1;
=﹣1;
(3)假设在线段AT上存在点M,使OM⊥AM,连接OM、OA,作MN⊥x轴于点N,如图2,∵c=1,∴C(1,4),F(0,4),P(1,![]() ),B(a,0),设直线BF的解析式为y=k′x+4,由题意可得:
),B(a,0),设直线BF的解析式为y=k′x+4,由题意可得: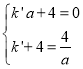 ,解得a=2,∴A(2,2),∴AP为△DCT的中位线,∴T(3,0),∴AT=
,解得a=2,∴A(2,2),∴AP为△DCT的中位线,∴T(3,0),∴AT=![]() =
=![]()
∵S△OAT=![]() OTAB=
OTAB=![]() ATOM,∴OM=
ATOM,∴OM=![]() =
=![]() =
=![]() ,在Rt△OMT中,MT=
,在Rt△OMT中,MT=![]() =
=![]() =
=![]() ,同理可求得MN=
,同理可求得MN=![]() =
=![]() ,在Rt△OMN中,ON=
,在Rt△OMN中,ON=![]() =
=![]() =
=![]() ,∵2<
,∵2<![]() <3,∴点M在线段AT上,即在线段AT上存在点M,使得OM⊥AM,M点的坐标为(
<3,∴点M在线段AT上,即在线段AT上存在点M,使得OM⊥AM,M点的坐标为(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图正方形ABCD中,E为BC上任意一点,过E作EF⊥BC,交BD于F,G为DF的中点,连AE和AG.
(1)如图1,求证:∠FEA+∠DAG=45°;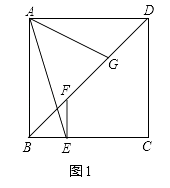
(2)如图2在(1)的条件下,设BD和AE的交点为H,BG=8,DH=9,求AD的长.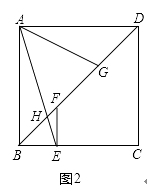
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着社会的发展,私家车变得越来越普及,使用节能低油耗汽车,对环保有着非常积极的意义,某市有关部门对本市的某一型号的若干辆汽车,进行了一项油耗抽样实验:即在同一条件下,被抽样的该型号汽车,在油耗1L的情况下,所行驶的路程(单位:km)进行统计分析,结果如图所示:

(注:记A为12~12.5,B为12.5~13,C为13~13.5,D为13.5~14,E为14~14.5)
请依据统计结果回答以下问题:
(1)试求进行该试验的车辆数;
(2)请补全频数分布直方图;
(3)若该市有这种型号的汽车约900辆(不考虑其他因素),请利用上述统计数据初步预测,该市约有多少辆该型号的汽车,在耗油1L的情况下可以行驶13km以上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学对数据26,36,46,5□,52进行统计分析,发现其中一个两位数的个位数字被黑水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.平均数B.中位数C.方差D.极差
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a2a3=a6
B.(﹣a)4=a4
C.a2+a3=a5
D.(a2)3=a5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系
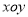 中,等边
中,等边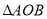 的边长为6,点
的边长为6,点 在边
在边 上,点
上,点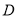 在边
在边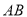 上,且
上,且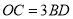 .反比例函数
.反比例函数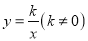 的图象恰好经过点
的图象恰好经过点 和点
和点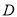 .则
.则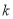 的值为 ( )
的值为 ( )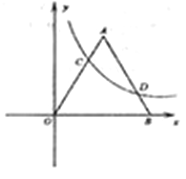
A.
 B.
B. 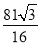 C.
C. 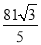 D.
D.
相关试题

