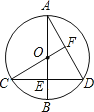
【题目】如图,已知⊙O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD
(1) 求证:E是OB的中点
(2) 若AB=8,求CD的长
参考答案:
【答案】(1)见解析;(2)4![]() .
.
【解析】试题分析:(1)要证明:E是OB的中点,只要求证OE=![]() OB=
OB=![]() OC,即证明∠OCE=30°即可.
OC,即证明∠OCE=30°即可.
(2)在直角△OCE中,根据勾股定理就可以解得CE的长,进而求出CD的长.
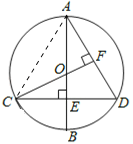
(1)证明:连接AC,如图
∵直径AB垂直于弦CD于点E,
∴![]() ,
,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即:△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,![]() ,
,
∴![]() ,
,
∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=8,
∴![]() ,
,
又∵BE=OE,
∴OE=2,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司打算至多用1200元印制广告单.已知制版费50元,每印一张广告单还需支付0.3元的印刷费,则该公司可印制的广告单数量x(张)满足的不等式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】 “已知:正比例函数y1=kx(k>0)与反比例函数y2=
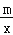 (m>0)图象相交于A、B两点,其横坐标分别是1和﹣1,求不等式kx>
(m>0)图象相交于A、B两点,其横坐标分别是1和﹣1,求不等式kx>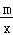 的解集.”对于这道题,某同学是这样解答的:“由图象可知:当x>1或﹣1<x<0时,y1>y2,所以不等式kx>
的解集.”对于这道题,某同学是这样解答的:“由图象可知:当x>1或﹣1<x<0时,y1>y2,所以不等式kx>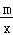 的解集是x>1或﹣1<x<0”.他这种解决问题的思路体现的数学思想方法是( )
的解集是x>1或﹣1<x<0”.他这种解决问题的思路体现的数学思想方法是( )A.数形结合 B.转化 C.类比 D.分类讨论
-
科目: 来源: 题型:
查看答案和解析>>【题目】房山某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下的两个统计图.请根据下面两个不完整的统计图回答以下问题:

(1)这次抽样调查中,共调查了 名学生;
(2)补全两幅统计图;
(3)根据抽样调查的结果,估算该校1000名学生中大约有多少人选择“小组合作学习”?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD、∠ABC的平分线AF、BG分别与线段CD交于点F、G,
AF与BG交于点E.

(1)求证:AF⊥BG,DF=CG;
(2)若AB=10,AD=6,AF=8,求FG和BG的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径r=3,设圆心O到一条直线的距离为d,圆上到这条直线的距离为2的点的个数为m,给出下列命题:
①若d>5,则m=0;②若d=5,则m=1;③若1<d<5,则m=3;④若d=1,则m=2;⑤若d<1,则m=4.
其中正确命题的个数是( )
A. 1 B. 2 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形具有而菱形不一定具有的性质是( )
A. 对角线相等B. 对角线互相垂直平分
C. 对角线平分一组对角D. 四条边相等
相关试题

