【题目】如图,己知抛物线经过点A(l, 0),B(一3,0),C(0,3)三点.
(1)求抛物线的解析式;
(2)在x轴下方的抛物线上,是否存在点M,使得![]() ?若存在求出M点的坐标;若不存在,请说明理由;
?若存在求出M点的坐标;若不存在,请说明理由;
(3)点P是位于直线BC上方的抛物线上的一个动点,是否存在点P,使![]() 的面积最大?若存在,求出P的坐标及
的面积最大?若存在,求出P的坐标及![]() 的最大值:若不存在,说明理由.
的最大值:若不存在,说明理由.

参考答案:
【答案】(1) ![]()
(2)M点的坐标为:(-4,-5),(2,-5).
(3)当![]() 时,
时, ![]() 最大,最大值为
最大,最大值为![]() 。
。
【解析】试题分析:(1)由抛物线经过三点,可设抛物线的解析式为![]() ,将A、B、C三点带入方程即可求得a、b、c的值;
,将A、B、C三点带入方程即可求得a、b、c的值;
(2)设存在点M(a,b),由题意可知, ![]() 以AB=4为底,则高为OC=3,因此
以AB=4为底,则高为OC=3,因此![]() =10 ,又在
=10 ,又在![]() 中,以AB=4为底,则高为
中,以AB=4为底,则高为![]() ,所以
,所以![]() =
=![]() ,因为M点在x轴的下方,故b<0,因此b=-5,又因为M在抛物线上,所以满足抛物线方程。代入得:
,因为M点在x轴的下方,故b<0,因此b=-5,又因为M在抛物线上,所以满足抛物线方程。代入得: ![]() ,解得,
,解得, ![]() ,即可得到M点的坐标;
,即可得到M点的坐标;
(3)连接PC、PB,过P作PR⊥x轴,交BC于点Q,可知当PQ有最大值时, ![]() 有最大值,由待定系数法求得直线BC的解析式,设出点P的坐标,进而得出Q点坐标,表示出 PQ的长度,求出最大值,即可解决问题.
有最大值,由待定系数法求得直线BC的解析式,设出点P的坐标,进而得出Q点坐标,表示出 PQ的长度,求出最大值,即可解决问题.
试题分析:(1)设抛物线方程为![]() ,
,
将A(l,0),B(-3,0),C(0,3)带入方程得: 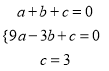 ,
,
解得 ,所以抛物线的解析式为:
,所以抛物线的解析式为: ![]() ;
;
(2)设存在点M(a,b),由题意可知, ![]() =
=![]() ×4×3=6,
×4×3=6,
∴![]() =
=![]() ,
, ![]() =5,
=5,
因为M点在x轴的下方,故b<0,因此b=-5,
又因为M在抛物线上,所以满足抛物线方程,
代入得: ![]() ,解得,
,解得, ![]() ,
,
所以M点的坐标为:(-4,-5),(2,-5).
(3)如图:
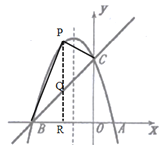
连接PC、PB,过P作PR⊥x轴,交BC于点Q,
设直线BC的解析式为:y=kx+m,把B(-3,0),C(0,3)代入,
则![]() ,
,
解得: ![]() ,
,
则直线BC的解析式是y=x+3.
设点P的坐标为(x, ![]() ),则Q坐标为(x
),则Q坐标为(x![]() ),
),
PQ=![]() =-(x+
=-(x+![]() )2+
)2+![]() ,
,
当x=-![]() 时,PQ有最大值
时,PQ有最大值![]() ,此时
,此时![]() 有最大值为:
有最大值为: ![]() ×
×![]() ×3=
×3=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式 a2-3a+1 的值为 0,则代数式-3a2+9a+4 的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】【回归课本】我们曾学习过一个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
【初步体验】
(1)如图1,在△ABC中,点D、F在AB上,E、G在AC上,DE∥FC∥BC.若AD=2,AE=1,DF=6,则EG= ,
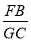 = .
= .(2)如图2,在△ABC 中,点D、F在AB上,E、G在AC上,且DE∥BC∥FG.以AD、DF、FB为边构造△ADM(即AM=BF,MD=DF);以AE、EG、GC为边构造△AEN(即AN=GC,NE=EG).
求证:∠M=∠N.
【深入探究】
上述基本事实启发我们可以用“平行线分线段成比例”解决下列问题:
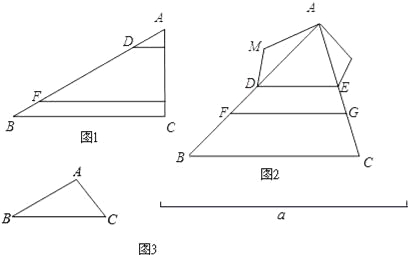
(3)如图3,已知△ABC和线段a,请用直尺与圆规作△A′B′C′.
满足:①△A′B′C′∽△ABC;②△A′B′C′的周长等于线段a的长度.(保留作图痕迹,并写出作图步骤)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC的平分线与BC的垂直平分线相交于点D.
(1)请你利用尺规作图作出点D;
(2)过点D作DE⊥AB于E,DF⊥AC于F,若AB=6,AC=3,则BE=________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句中是命题的有( )
①如果两个角都等于70°,那么这两个角是对顶角; ②三角形内角和等于180°; ③画线段AB=3 cm.
A. 0个B. 1个C. 2个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,抛物线的顶点D的坐标为(1,-4),且与y轴交于点
C(0,3)
求该函数的关系式;
求改抛物线与x轴的交点A,B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题:
为了响应市政府“绿色出行”的号召,小张上下班由自驾车方式改为骑自行车方式.已知小张单位与他家相距20千米,上下班高峰时段,自驾车的平均速度是自行平均车速度的2倍,骑自行车所用时间比自驾车所用时间多
 小时.求自驾车平均速度和自行车平均速度各是多少?
小时.求自驾车平均速度和自行车平均速度各是多少?
相关试题

