【题目】8月25日,高德公司发布了《2015年第二季度中国主要城市交通分析报告》,在国内城市拥堵排行中,北京、杭州、广州位列前三,山城重庆排第九.为了解重庆市交通拥堵情况,经调查统计:菜园坝长江大桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的一次函数,且满足v=﹣ ![]() x+88(其中20≤x≤220).
x+88(其中20≤x≤220).
(1)在交通高峰时段,为使菜园坝长江大桥上车流速度不小于48千米/时且不大于60千米/时,应控制
菜园坝长江大桥上的车流密度在什么范围内?
(2)若规定车流量(单位:辆/时)是单位时间内通过桥上某观测点的车辆数.即:车流量=车流速度×车
流密度.那在(1)的条件下.菜园坝长江大桥上车流量的最大值是多少?
(3)当车流量为4680辆/时时,为了使桥上的更畅通,则桥上的车流密度应为多少?
参考答案:
【答案】
(1)解:由题意,得 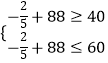 ,
,
解得:70≤x≤120.
故应控制大桥上的车流密度在70≤x≤120范围内
(2)解:设车流量y与x之间的关系式为y=vx,
当70≤x≤120时
y=(﹣ ![]() x+88)x=﹣
x+88)x=﹣ ![]() (x﹣110)2+4840,
(x﹣110)2+4840,
∴当x=110时,y最大=4840.
∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆
(3)解:当y=4680时,即4680=﹣ ![]() (x﹣110)2+4840,
(x﹣110)2+4840,
解得:x=130,或x=90,
故当车流量为4680辆/时时,为了使桥上的更畅通,则桥上的车流密度应为130辆/千米,或90辆/千米
【解析】(1)根据题意得方程组即可得到结论;(2)设车流量y与x之间的关系式为y=vx,当70≤x≤120时求得函数关系,由函数的性质就可以求出结论;(3)当y=4680时,列方程即可得到结论.
【考点精析】解答此题的关键在于理解一元一次不等式组的应用的相关知识,掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2﹣4x﹣5=0.
-
科目: 来源: 题型:
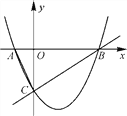
查看答案和解析>>【题目】如图,已知直线
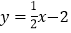 与x轴交于点B,与y轴交于点C,抛物线
与x轴交于点B,与y轴交于点C,抛物线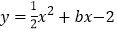
与x轴交于A、B两点(A在B的左侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)点M是上述抛物线上一点,如果△ABM和△ABC相似,求点M的坐标;
(3)连接AC,求顶点D、E、F、G在△ABC各边上的矩形DEFC面积最大时,写出该矩形在AB边上的顶点的坐标.
-
科目: 来源: 题型:
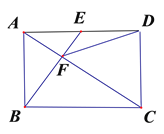
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,
(1)求证:CF=2AF;
(2)求tan∠CFD的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数a,b满足(2a+1)2+|a+b+1|=0,且关于x,y的方程组
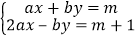 的解x<0,y>0,求m的取值范围.
的解x<0,y>0,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】将两个底边相等的等腰三角形按照图所示的方式拼接在一起(隐藏互相重合的底边)的图形俗称为“筝形”.假如“筝形”下个定义,那么下面四种说法中,你认为最能够描述“筝形”特征的是 ( )
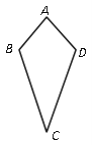
A. 有两组邻边相等的四边形称为“筝形”;
B. 有两组对角分别相等的四边形称为“筝形”;
C. 两条对角线互相垂直的四边形称为“筝形”;
D. 以一条对角线所在直线为对称轴的四边形称为“筝形”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式﹣4x≥﹣12的正整数解为 .
相关试题

