【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

参考答案:
【答案】见解析(2)![]()
【解析】
(1)根据三角形中位线定理和全等三角形的判定证明即可;
(2)利用正方形的性质和矩形的面积公式解答即可.
(1)连接EF,∵点F,G,H分别是BC,BE,CE的中点,
∴FH∥BE,FH=![]() BE,FH=BG,
BE,FH=BG,
∴∠CFH=∠CBG,
∵BF=CF,
∴△BGF≌△FHC,
(2)当四边形EGFH是正方形时,连接GH,可得:EF⊥GH且EF=GH,

∵在△BEC中,点G,H分别是BE,CE的中点,
∴![]() 且GH∥BC,
且GH∥BC,
∴EF⊥BC,
∵AD∥BC,AB⊥BC,
∴AB=EF=GH=![]() a,
a,
∴矩形ABCD的面积=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为

A.
 B. 5C. 3D.
B. 5C. 3D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
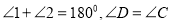 ,求证:
,求证: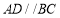 ,请将证明过程填写完整.
,请将证明过程填写完整.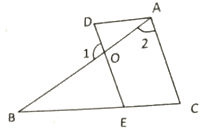
证明:∵
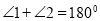 (已知)
(已知)又∵
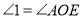 ( )
( )∴________
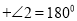 ,
,∴
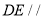 ____________( )
____________( )∴
 ______________( )
______________( )又∵
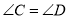 (已知)
(已知)∴
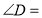 ________________,
________________,∴
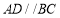 ( )
( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:我们把对角线相等的四边形叫做和美四边形.
 请举出一种你所学过的特殊四边形中是和美四边形的例子.
请举出一种你所学过的特殊四边形中是和美四边形的例子. 如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形; 如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,
如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O, ,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).

(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈
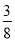 ,cos22°≈
,cos22°≈ ,tan22°≈
,tan22°≈ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某社区要调查社区居民双休日的体育锻炼情况,采用下列调查方式:
A.从一幢高层住宅楼中选取200名居民;
B.从不同住宅楼中随机选取200居民;
C.选取社区内200名在校学生
(1)上述调查方式最合理的是___________________;
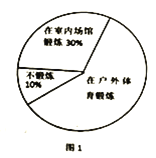
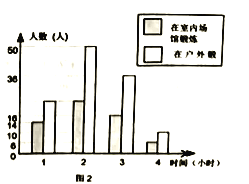
(2)将最合理的调查方式得到的数据制成扇形统计图(如图1)和频数分布直方图(如图2).在这个调查中,200名居民双休日在户外体育锻炼的有_____________人;
(3)调查中的200名居民在户外锻炼1小时的人数为__________________;
(4)请你估计该社区1600名居民双休日体育锻炼时间不少于3小时的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有三个点
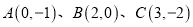 ,
,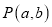 是
是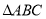 的边
的边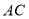 上一点,
上一点,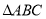 经平移后得到
经平移后得到 ,点
,点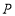 的对应点为
的对应点为 .
.(1)画出平移后的
 ,写出点
,写出点 的坐标;
的坐标;(2)
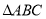 的面积为_________________;
的面积为_________________;(3)若点
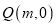 是
是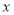 轴上一动点,
轴上一动点,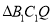 的面积为
的面积为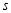 ,求
,求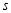 与
与 之间的关系式(用含
之间的关系式(用含 的式子表示
的式子表示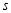 )
)
相关试题

