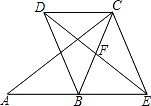
【题目】如图①,在正方形ABCD中,F是对角线AC上的一点,点E在BC的延长线上,且BF=EF. 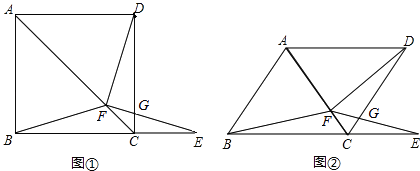
(1)求证:BF=DF;
(2)求证:∠DFE=90°;
(3)如果把正方形ABCD改为菱形,其他条件不变(如图②),当∠ABC=50°时,∠DFE=度.
参考答案:
【答案】
(1)证明:在正方形ABCD中,BC=DC,∠BCF=∠DCF=45°,
∵在△BCF和△DCF中,
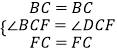 ,
,
∴△BCF≌△DCF(SAS);
∴BF=DF
(2)证明:∵BF=EF,
∴∠FBE=∠FEB,
又∵∠FBE=∠FDC,
∴∠FEB=∠FDC,
又∵∠DGF=∠EGC,
∴∠DFG=∠ECG=90°,
即∠DFE=90°
(3)50
【解析】(3)证明:由(1)知,△BCF≌△DCF, ∴∠CBF=∠CDF,
∵EE=FB,
∴∠CBF=∠E,
∵∠DGF=∠EGC(对顶角相等),
∴180°﹣∠DGF﹣∠CDF=180°﹣∠EGC﹣∠E,
即∠DFE=∠DCE,
∵AB∥CD,
∴∠DCE=∠ABC,
∴∠DFE=∠ABC=50°,
所以答案是:50.
【考点精析】利用菱形的性质和正方形的性质对题目进行判断即可得到答案,需要熟知菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,∠BCD的三等分线是CP,CQ,又CR⊥CP,若∠B=78°,则∠RCE=( )
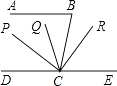
A.66°
B.65°
C.58°
D.56° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1 , A2 , A3 , A4 , …表示,则顶点A55的坐标是( )

A.(13,13)
B.(﹣13,﹣13)
C.(14,14)
D.(﹣14,﹣14) -
科目: 来源: 题型:
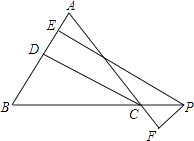
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,PE⊥AB,PF⊥AC,CD⊥AB,垂足分别为E、D、F,求证:PE﹣PF=CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点F是BC的中点,点E是线段AB的延长线上的一动点,连接EF,过点C作AB的平行线CD,与线段EF的延长线交于点D,连接CE、BD.
(1)求证:四边形DBEC是平行四边形.
(2)若∠ABC=120°,AB=BC=4,则在点E的运动过程中: ①当BE=时,四边形BECD是矩形,试说明理由;
②当BE=时,四边形BECD是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2)2n+1+2(﹣2)2n=_____.
-
科目: 来源: 题型:
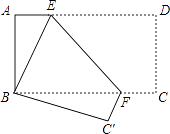
查看答案和解析>>【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为度.
相关试题

