【题目】在矩形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在矩形外部作
为边在矩形外部作![]() ,且
,且![]() ,连接
,连接![]() ,则
,则![]() 的最小值为___________.
的最小值为___________.

参考答案:
【答案】![]()
【解析】由S△ABP=![]() ABh=15,得出三角形的高h=5,在直线AB外作直线l∥AB,且两直线间的距离为5,延长DA至M使AM=10,则M、A关于直线l对称,连接CM,交直线l于P,连接AP、BP,则S△ABP=15,此时AP+CP=CM,根据两点之间线段最短可知AP+CP的最小值为CM;然后根据勾股定理即可求得.
ABh=15,得出三角形的高h=5,在直线AB外作直线l∥AB,且两直线间的距离为5,延长DA至M使AM=10,则M、A关于直线l对称,连接CM,交直线l于P,连接AP、BP,则S△ABP=15,此时AP+CP=CM,根据两点之间线段最短可知AP+CP的最小值为CM;然后根据勾股定理即可求得.
详解;∵在矩形ABCD中,AB=6,BC=8,
S△ABP=![]() ABh=15,
ABh=15,
∴h=5,
在直线AB外作直线l∥AB,且两直线间的距离为5,延长DA至M使AM=10,则M、A关于直线l对称,连接CM,交直线l于P,连接AP、BP,则S△ABP=15,此时AP+CP=CM,根据两点之间线段最短可知AP+CP的最小值为CM;

∵AD=8,AM=10,
∴DM=18,
∵CD=6,
∴CM=![]() ,
,
∴AP+CP的最小值为![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中,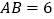 ,点
,点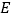 在边
在边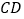 上,且
上,且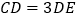 ,将
,将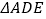 沿
沿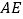 对折至
对折至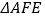 ,延长
,延长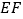 交边
交边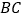 于点
于点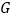 ,连接
,连接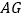 、
、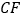 .则下列结论:①
.则下列结论:①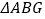 ≌
≌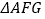 ;②
;②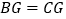 ;③
;③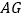 ∥
∥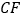 ;④
;④ .其中正确的是( )
.其中正确的是( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简计算
(1)解不等式组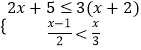 ;
;
(2)先化简,再求值: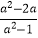 ÷(a﹣1﹣
÷(a﹣1﹣  ),其中a是方程x2+x=6的一个根.
),其中a是方程x2+x=6的一个根. -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
甲、乙两人同时从相距25千米的A地去B 地,甲骑车乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40分钟,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】人民网为了解百姓对时事政治关心程度,特对18~35岁的青年人每天发微博数量进行调查,设一个人的“日均发微博条数”为m,规定:当m≥10时为甲级,当5≤m<10时为乙级,当0≤m<5时为丙级,现随机抽取20个符合年龄条件的青年人开展调查,所抽青年人的“日均发微博条数”的数据如下:
0
8
2
8
10
13
7
5
7
3
12
10
7
11
3
6
8
14
15
12
(1)样本数据中为甲级的频率为;(直接填空)
(2)求样本中乙级数据的中位数和众数.
(3)从样本数据为丙级的人中随机抽取2人,用列举法或树状图求抽得2个人的“日均发微博条数”都是3的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是马小哈同学做的一道题:
解方程:
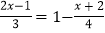
解:①去分母,得 4(2x﹣1)=1﹣3(x+2)
②去括号,得 8x﹣4=1﹣3x﹣6
③移项,得8x+3x=1﹣6+4
④合并同类项,得 11x=﹣1
⑤系数化为1,得

(1)上面的解题过程中最早出现错误的步骤是(填代号) ;
(2)请在本题右边正确的解方程:
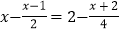 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】从南京站开往上海站的一辆和谐号动车,中途只停靠苏州站,甲、乙、丙3名互不相识的旅客同时从南京站上车.
(1)求甲、乙、丙三名旅客在同一个站下车的概率;
(2)求甲、乙、丙三名旅客中至少有一人在苏州站下车的概率.
相关试题

