【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .则下列结论:①
.则下列结论:①![]() ≌
≌![]() ;②
;②![]() ;③
;③![]() ∥
∥![]() ;④
;④![]() .其中正确的是( )
.其中正确的是( )

A. ①② B. ①②③ C. ①②④ D. ①②③④
参考答案:
【答案】B
【解析】根据翻折变换的性质和正方形的性质可证△ABG≌△AFG;在直角△ECG中,根据勾股定理可证BG=GC;通过证明∠AGB=∠AGF=∠GFC=∠GCF,由平行线的判定可得AG∥CF;由于S△FGC=S△GCE-S△FEC,求得面积比较即可.
①正确.因为AB=AD=AF,AG=AG,∠B=∠AFG=90°,∴△ABG≌△AFG;
②正确.因为:EF=DE=![]() CD=2,设BG=FG=x,则CG=6-x.在直角△ECG中,根据勾股定理,得(6-x)2+42=(x+2)2,解得x=3.所以BG=3=6-3=GC;
CD=2,设BG=FG=x,则CG=6-x.在直角△ECG中,根据勾股定理,得(6-x)2+42=(x+2)2,解得x=3.所以BG=3=6-3=GC;
③正确.因为CG=BG=GF,所以△FGC是等腰三角形,∠GFC=∠GCF.又∠AGB=∠AGF,∠AGB+∠AGF=180°-∠FGC=∠GFC+∠GCF,
∴∠AGB=∠AGF=∠GFC=∠GCF,∴AG∥CF;
④错误.过F作FH⊥DC,
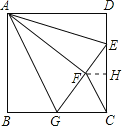
∵BC⊥DH,
∴FH∥GC,
∴△EFH∽△EGC,
∴![]() ,
,
EF=DE=2,GF=3,
∴EG=5,
∴△EFH∽△EGC,
∴相似比为:![]() ,
,
∴S△FGC=S△GCE-S△FEC=![]() ×3×4-
×3×4-![]() ×4×(
×4×(![]() ×3)=
×3)=![]() .
.
而S△AFE=S△ADE=![]() ,
,
∴S△FGC≠S△AFE
故答案为:①②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为
 a的正方形ABCD和边长为
a的正方形ABCD和边长为  b的正方形BEFG排放在一起,O1和O2分别是这两个正方形的中心,则阴影部分的面积为 .
b的正方形BEFG排放在一起,O1和O2分别是这两个正方形的中心,则阴影部分的面积为 . 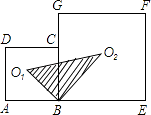
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,航空母舰始终以40千米/时的速度由西向东航行,飞机以800千米/时的速度从舰上起飞,向西航行执行任务,如果飞机在空中最多能连续飞行4个小时,那么它在起飞_____小时后就必须返航,才能安全停在舰上?

-
科目: 来源: 题型:
查看答案和解析>>【题目】列一元一次方程解应用题.
(1)商店出售茶壶和茶杯,茶壶每只定价20元,茶杯每只定价5元,该商品制定了两种优惠方法:
①买一只茶壶赠一只茶杯;②按总价的90%付款.某顾客购买茶壶5只,茶杯若干只(不少于5只),问顾客买多少只茶杯时,两种方法付款相同.假如该顾客买了茶杯20只,哪种买法实惠?
(2)某人原计划骑车以每小时12千米的速度由A地到B地,这样便可在规定的时间到达,但他因事将原计划出发的时间推迟了20分钟,只好以每小时15千米的速度前进,结果比规定时间早4分钟到达B地,求A,B两地间的距离.
(3)某工厂完成一批产品,一车间单独完成需30天,二车间单独完成需20天.
①如一车间先做若干天,然后由二车间继续做,直至完成,前后共做了25天,问一车间先做了几天?
②如一车间先做了3天后,二车间加入一起做,还需多少天才能完成?
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简计算
(1)解不等式组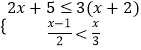 ;
;
(2)先化简,再求值: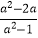 ÷(a﹣1﹣
÷(a﹣1﹣  ),其中a是方程x2+x=6的一个根.
),其中a是方程x2+x=6的一个根. -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
甲、乙两人同时从相距25千米的A地去B 地,甲骑车乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40分钟,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形
 中,
中, ,
, ,以
,以 为边在矩形外部作
为边在矩形外部作 ,且
,且 ,连接
,连接 ,则
,则 的最小值为___________.
的最小值为___________.
相关试题

