【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°
求证:△AEF≌△BCF.

参考答案:
【答案】证明见解析.
【解析】试题分析:根据垂直定义求出∠AFB=∠BFC=∠ADB=90°,求出∠CBF=∠EAF,根据等腰三角形的判定推出AF=BF,根据ASA推出两三角形全等即可.
证明:∵AD⊥BC,BF⊥AC,
∴∠AFB=∠BFC=∠ADB=90°,
∴∠C+∠CBF=90°,∠C+∠EAF=90°,
∴∠CBF=∠EAF,
∵∠AFB=90°,∠BAC=45°,
∴∠ABF=∠BAF=45°,
∴AF=BF,
在△AEF和△BCF中,
∠EAF=∠CBFAF=BF∠AFE=∠BFC,
∴△AEF≌△BCF(SAS).
-
科目: 来源: 题型:
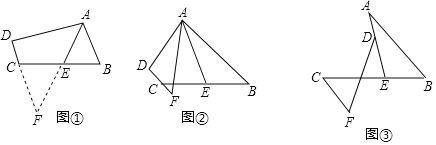
查看答案和解析>>【题目】(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为 ;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知A(1,-5),B(4,2),C(-1,0)三点.
(1)点B关于x轴对称点B′的坐标为 ,点C关于y轴对称点C′的坐标为 ;
(2)求(1)中的△AB′C′的面积.
-
科目: 来源: 题型:
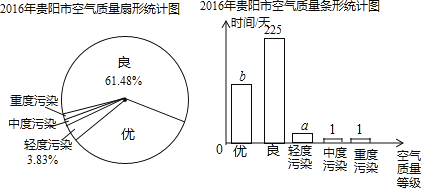
查看答案和解析>>【题目】2017年6月2日,贵阳市生态委发布了《2016年贵阳市环境状况公报》,公报显示,2016年贵阳市生态环境质量进一步提升,小颖根据公报中的部分数据,制成了下面两幅统计图,请根据图中提供的信息,回答下列问题:
(1)a= ,b= ;(结果保留整数)
(2)求空气质量等级为“优”在扇形统计图中所占的圆心角的度数;(结果精确到1°)
(3)根据了解,今年1~5月贵阳市空气质量优良天数为142天,优良率为94%,与2016年全年的优良率相比,今年前五个月贵阳市空气质量的优良率是提高还是降低了?请对改善贵阳市空气质量提一条合理化建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商家购进A、B两种商品,A种商品用了480元,B种商品用了1260元,A、B两种商品的数量比为1﹕3,A种商品每千克的进价比B种商品每千克的进价多2元.A、B两种商品各购进多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式4x﹣x3因式分解的结果是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数,把它的个位数字与十位数字交换位置得到新两位数,原两位数的个位数字比原两位数的十位数字大2,且新两位数与原两位数的和为154,求原两位数是多少?
相关试题

