【题目】如图,二次函数![]() 的图象经过坐标原点,与
的图象经过坐标原点,与![]() 轴的另一个交点为A(-2,0).
轴的另一个交点为A(-2,0).

(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)y=-x2-2x(2)![]() 或
或![]()
【解析】阿济格:(1)把点(0,0)和点A(-2,0)分别代入函数关系式来求b、c的值;
(2)设点P的坐标为(x,-x2-2x).利用三角形的面积公式得到-x2-2x=±3.通过解方程来求x的值,则易求点P的坐标.
试题解析:(1)∵二次函数y=-x2+bx+c的图象经过坐标原点(0,0)
∴c=0.
又∵二次函数y=-x2+bx+c的图象过点A(-2,0)
∴-(-2)2-2b+0=0,
∴b=-2.
∴所求b、c值分别为-2,0;
(2)存在一点P,满足S△AOP=3.
设点P的坐标为(x,-x2-2x)
∵S△AOP=3
∴![]() ×2×|-x2-2x|=3
×2×|-x2-2x|=3
∴-x2-2x=±3.
当-x2-2x=3时,此方程无解;
当-x2-2x=-3时,
解得 x1=-3,x2=1.
∴点P的坐标为(-3,-3)或(1,-3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(a+2b)(3a﹣b)﹣(2a﹣b)(a+6b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(3x﹣y)2﹣(2x+y)2+5x(y﹣x)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).

(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠COA=90°,∠COD比∠DOA大28°,且OB是∠COA的平分线.
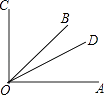
(1)求∠BOD的度数;
(2)将已知条件中的28°改为32°,则∠BOD=;
(3)将已知条件中的28°改为n°,则∠BOD= . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=x 2经变换后得到抛物线y=x 2+2,则这个变换可以( )
A.向左平移2个单位B.向上平移2个单位
C.向下平移2个单位D.向右平移2个单位
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.
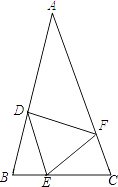
(1)求证:△DEF是等腰三角形;
(2)求证:∠B=∠DEF;
(3)当∠A=40°时,求∠DEF的度数.
相关试题

