【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE. 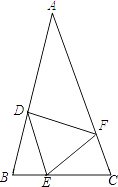
(1)求证:△DEF是等腰三角形;
(2)求证:∠B=∠DEF;
(3)当∠A=40°时,求∠DEF的度数.
参考答案:
【答案】
(1)证明:∵AB=AC,
∴∠B=∠C,
在△DBE和△ECF中, 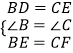 ,
,
∴△DBE≌△ECF,
∴DE=FE,
∴△DEF是等腰三角形
(2)证明:∵△BDE≌△CEF,
∴∠FEC=∠BDE,
∴∠DEF=180°﹣∠BED﹣∠EFC=180°﹣∠DEB﹣∠EDB=∠B
(3)证明:∵由(2)知△BDE≌△CEF,
∴∠BDE=∠CEF,
∴∠CEF+∠DEF=∠BDE+∠B,
∴∠DEF=∠B,
∴AB=AC,∠A=40°,
∴∠DEF=∠B= ![]() =70°
=70°
【解析】(1)首先根据条件证明△DBE≌△ECF,根据全等三角形的性质可得DE=FE,进而可得到△DEF是等腰三角形;(2)根据△BDE≌△CEF,可知∠FEC=∠BDE,∠DEF=180°﹣∠BED﹣∠EFC=180°﹣∠DEB﹣∠EDB=∠B即可得出结论;(3)由(2)知∠DEF=∠B,再根据等腰三角形的性质即可得出∠DEF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 的图象经过坐标原点,与
的图象经过坐标原点,与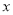 轴的另一个交点为A(-2,0).
轴的另一个交点为A(-2,0).
(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠COA=90°,∠COD比∠DOA大28°,且OB是∠COA的平分线.
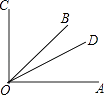
(1)求∠BOD的度数;
(2)将已知条件中的28°改为32°,则∠BOD=;
(3)将已知条件中的28°改为n°,则∠BOD= . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=x 2经变换后得到抛物线y=x 2+2,则这个变换可以( )
A.向左平移2个单位B.向上平移2个单位
C.向下平移2个单位D.向右平移2个单位
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.﹣a是负数
B.分数都是有理数
C.有理数不是正数就是负数
D.绝对值等于本身的数是正数 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级四个班级的学生义务为校植树.一班植树x棵,二班植树的棵树比一班的2倍少40棵,三班植树的棵数比二班的一半多30棵,四班植树的棵数比三班的一半多20棵.
(1)求四个班共植树多少棵?(用含x的式子表示)
(2)若三班和四班植树一样多,那么植树最多的班级比植树最少的班级多植树多少棵? -
科目: 来源: 题型:
查看答案和解析>>【题目】对于下列各式,其中错误的是( )
A.(﹣1)2015=﹣1
B.﹣12016=﹣1
C.(﹣3)2=6
D.﹣(﹣2)3=8
相关试题

