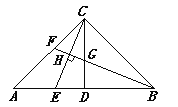
【题目】如图,在△ABC中,CD是中线,∠ACB=90°,AC=BC,点E,F分别为AB,AC上的动点(均不与端点重合),且CE⊥BF,垂足为H,BF与CD相交于G.
(1)求证:AE=CG;
(2)当线段AE,CF之间满足什么数量关系时,BF为△ABC的角平分线?请说明理由.
参考答案:
【答案】(1)证明见解析;(2)当AE=CF时,BF为△ABC的角平分线.理由见解析.
【解析】试题分析:
(1)由等腰直角三角形的性质可证得∠A=∠BCG=45°,再由∠ACE+∠BCE=90°,∠CBG+∠BCE=90°,得到∠ACE=∠CBG,这样结合AC=BC,由“ASA”可证△ACE≌△CBG就可得到结论了;
(2)当AE=CF时,BF是△ABC的角平分线;由AE=CF,AE=CG,可得CF=CG,这样∠CFG=∠CGF,进一步就可证得∠CBF=∠DBF,从而可得BF平分∠ABC.
试题解析:
(1)∵∠ACB=90°,AC=BC,CD是中线,
∴∠ACE+∠BCE=90°,∠A=∠ABC=∠BCG=45°.
∵CE⊥BF,垂足为H,∴∠BHC=90°.
∴∠CBG+∠BCE=90°.
∴∠ACE=∠CBG.
在△ACE和△CBG中: 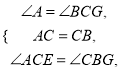
∴△ACE≌△CBG.
∴AE=CG.
(2)当AE=CF时,BF为△ABC的角平分线.
理由如下:∵AE=CF,AE=CG.
∴CF=CG.
∴∠CFG=∠CGF.
∵∠CFG=∠A+∠ABF,∠CGF=∠BCG+∠CBF,∠A=∠BCG,
∴∠ABF=∠CBF.即BF为△ABC的角平分线.
-
科目: 来源: 题型:
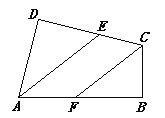
查看答案和解析>>【题目】如图,在四边形ABCD中, ∠B=∠D=90°,∠DAB与∠DCB 的平分线分别交DC,AB于E,F.求证:AE∥CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系的第二象限内有一点P,点P到x轴的距离为2,到y轴的距离为3,则点P的坐标是( )
A.(-3,2)B.(3,-2)C.(2,-3)D.(-2,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a既不是正数,也不是负数,b是最小的正整数,c表示下列一组数:
-2,1.5,0,130%, ,860,-3.4中非正数的个数,则a+b+c等于多少?
,860,-3.4中非正数的个数,则a+b+c等于多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】两条直线被第三条直线所截,如果∠1和∠2是同旁内角,且∠1=75°,那么∠2为( )
A.75°
B.105°
C.75°或105°
D.大小不定 -
科目: 来源: 题型:
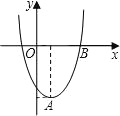
查看答案和解析>>【题目】在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
相关试题

