【题目】列一元一次方程解应用题:
某管道由甲、乙两工程队单独施工分别需要30天、20天.
(1)如果两队从管道两端同时施工,需要多少天完工?
(2)又知甲队单独施工每天需付200元施工费,乙队单独施工每天需付280元施工费,那么是由甲队单独施工,还是由乙队单独施工,还是由两队同时施工?请你按照少花钱多办事的原则,设计一个方案,并通过计算说明理由.
参考答案:
【答案】(1)需要12天完工;(2)由乙队单独施工花钱少,理由见解析.
【解析】试题分析:(1)设需要x天完工,根据等量关系:施工效率×时间=工作总量,列方程进行求解即可;
(2)分三种情况:甲单独、乙单独、甲乙合作,分别求出每种情况的费用,进行比较即可得出施工费用最少的那个方案.
试题解析:(1)设需要x天完工,由题意得![]() x+
x+![]() x=1 ,
x=1 ,
解得:x=12 ,
答:需要12天完工;
(2)由乙队单独施工花钱少,
理由:甲单独施工需付费:200×30=6000(元),
乙单独施工需付费:280×20=5600(元),
两队同时施工需付费:(200+280)×12=5760(元),
因为5600<5760<6000, 所以由乙队单独施工花钱少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,AC=8,BD=6,DH⊥AB于H.
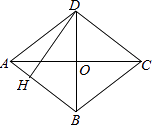
求:
(1)菱形ABCD的周长;
(2)求DH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:
(1)3(x2-2x-1)-4(3x-2)+2(x-1),其中x=﹣3;
(2)2a2﹣[
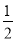 (ab﹣4a2)+8ab]﹣
(ab﹣4a2)+8ab]﹣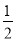 ab,其中a=1,b=
ab,其中a=1,b=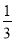 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=
 .
.(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;
(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
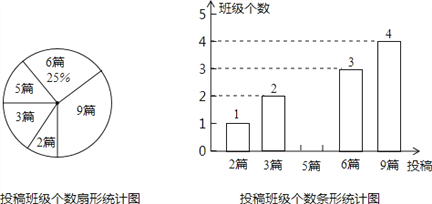
查看答案和解析>>【题目】为积极响应市政府提出的“建设美丽南宁”的号召,我市某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
(1)求扇形统计图中投稿篇数为2所对应的扇形的圆心角的度数:
(2)求该校八,九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数为9篇的四个班级中,八,九年级各有两个班,校学生会准备从这四个班中选出两个班参加全市的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a2·a3=a6
B.(a2)3=a5
C.(-2a2b)3=-8a6b3
D.(2a+1)2=4a2+2a+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】清晨蜗牛从树根沿着树干往上爬,树高10m,白天爬4m,夜间下滑3m,它从树根爬上树顶,需( )
A.10天
B.9天
C.8天
D.7天
相关试题

