【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

请回答:BC+DE的值为________
参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数________
参考答案:
【答案】 ![]() 60°
60°
【解析】试题分析:请回答:由图2及其做法可得:EF=CD=3,CF=DE,所以BC+DE=BF,在Rt△BEF中由勾股定理可得BF=![]() ;解决问题:连接AE,CE,可证得四边形DCEF是平行四边形,四边形DCEF是平行四边形,进而可证△ACE是等边三角形,从而得∠AGF=∠ACE=60°.
;解决问题:连接AE,CE,可证得四边形DCEF是平行四边形,四边形DCEF是平行四边形,进而可证△ACE是等边三角形,从而得∠AGF=∠ACE=60°.
试题解析:解:BC+DE的值为![]() . 2分
. 2分
解决问题:
连接AE,CE,如图.
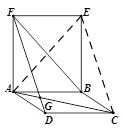
∵四边形ABCD是平行四边形,
∴AB //DC.
∵四边形ABEF是矩形,
∴AB //FE,BF=AE.
∴DC //FE.
∴四边形DCEF是平行四边形. 3分
∴CE //DF.
∵AC=BF=DF,
∴AC=AE=CE.
∴△ACE是等边三角形. 4分
∴∠ACE=60°.
∵CE∥DF,
∴∠AGF=∠ACE=60°. 5分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数a,b满足ab<0,a+b>0,7a+2b+1=﹣|b﹣a|,则
 的值为_____.
的值为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】某村庄计划建造A,B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积和可供使用农户数见下表:
型号
占地面积
(单位:m2/个)
可供使用农户数
(单位:户/个)
A
15
18
B
20
30
已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.
(1)如何合理分配建造A,B型号“沼气池”的个数才能满足条件?满足条件的方案有几种?通过计算分别写出各种方案.
(2)请写出建造A、B两种型号的“沼气池”的总费用y和建造A型“沼气池”个数x之间的函数关系式;
(3)若A型号“沼气池”每个造价2万元,B型号“沼气池”每个造价3万元,试说明在(1)中的各种建造方案中,哪种建造方案最省钱,最少的费用需要多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“端午节”所示我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅棕、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不用口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个恰好吃到的是C粽的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC、BD相交于点O,E、F是AD、BC的中点,EF分别交AC、BD于M、N,且OM=ON.
求证:AC=BD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离为|4﹣1|= ;表示5和﹣2两点之间的距离为|5﹣(﹣2)|=|5+2|= ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|,如果表示数a和﹣2的两点之间的距离是3,那么a= .
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a= 时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】现用
 根长度相同的火柴棒,按如图①摆放时可摆成
根长度相同的火柴棒,按如图①摆放时可摆成 个正方形,按如图②摆放时可摆成
个正方形,按如图②摆放时可摆成 个正方形
个正方形(1)如图①,当
 时,
时, ___________,如图②,当
___________,如图②,当 时,
时, ________________;
________________;(2)
 与
与 之间有何数量关系,请你写出来并说明理由;
之间有何数量关系,请你写出来并说明理由;(3)现有61根火柴棒,现用若干根火柴棒摆成图①的形状后,剩下的火柴棒刚好可以摆成图②的形状。请你直接写出一种摆放方法,并通过计算验证你的结论


相关试题

