【题目】某村庄计划建造A,B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积和可供使用农户数见下表:
型号 | 占地面积 (单位:m2/个) | 可供使用农户数 (单位:户/个) |
A | 15 | 18 |
B | 20 | 30 |
已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.
(1)如何合理分配建造A,B型号“沼气池”的个数才能满足条件?满足条件的方案有几种?通过计算分别写出各种方案.
(2)请写出建造A、B两种型号的“沼气池”的总费用y和建造A型“沼气池”个数x之间的函数关系式;
(3)若A型号“沼气池”每个造价2万元,B型号“沼气池”每个造价3万元,试说明在(1)中的各种建造方案中,哪种建造方案最省钱,最少的费用需要多少万元?
参考答案:
【答案】(1)方案一:A型7个,B型13个;方案二:A型8个,B型12个;方案三:A型9个,B型11个;(2)y=-x+60;(3)方案三最省钱,需要的费用为51万元.
【解析】分析:(1)设该村计划修建A种沼气池x个,则修建B种沼气池(20-x)个,根据沼气池的占地面积和该村农户的数量建立不等式组求出其解即可;(2)根据表格信息即可得出y与x之间的函数关系式.(3)根据(2)的关系式及一次函数的增减性,结合(1)中x的取值范围即可求解.
详解:
(1)设建造A型沼气池x个,则建造B型沼气池(20-x)个,
依题意得:
![]() ,
,
解得:7≤x≤9.
∵x为整数∴x=7,8,9,
∴满足条件的方案有三种:
方案一:A型7个,B型13个;
方案二:A型8个,B型12个;
方案三:A型9个,B型11个;
(2)建造A、B两种型号的“沼气池”的总费用y和建造A型“沼气池”个数x之间的函数关系式为:y=2x+3(20-x)=-x+60;
(3)∵y=-x+60,为减函数,
∴当x取最大时,费用最少,
故可得方案三最省钱,需要51万元.
答:方案三最省钱,需要的费用为51万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示.
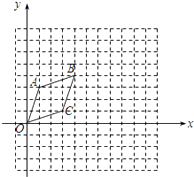
(I)以O为位似中心,在第一象限内将菱形OABC放大为原来的2倍得到菱形OA1B1C1 , 请画出菱形OA1B1C1 , 并直接写出点B1的坐标;
(II)将菱形OABC绕原点O顺时针旋转90°菱形OA2B2C2 , 请画出菱形OA2B2C2 , 并求出点B旋转到点B2的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E是BC上一点,直线AE交BD于点M,交DC的延长线于点F,G是EF的中点,连结CG.求证: ①△ABM≌△CBM;
②CG⊥CM.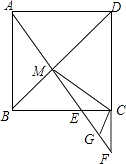
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数a,b满足ab<0,a+b>0,7a+2b+1=﹣|b﹣a|,则
 的值为_____.
的值为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】“端午节”所示我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅棕、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不用口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个恰好吃到的是C粽的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

请回答:BC+DE的值为________
参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC、BD相交于点O,E、F是AD、BC的中点,EF分别交AC、BD于M、N,且OM=ON.
求证:AC=BD.

相关试题

