【题目】已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P.

(1)求证:△AEB≌△CDA;
(2)求∠BPQ的度数;
(3)若BQ⊥AD于Q,PQ=6,PE=2,求BE的长.
参考答案:
【答案】(1)见解析;(2)60°;(3)14
【解析】
(1)根据等边三角形的性质,通过全等三角形的判定定理SAS证得结论;
(2)利用(1)中的全等三角形的对应角相等和三角形外角的性质,即可求得∠BPQ=60°;
(3)利用(2)的结果求得∠PBQ=30°,所以由“30度角所对的直角边是斜边的一半”得到2PQ=BP=12,则易求BE=BP+PE=14.
(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠C=60°,AB=CA,
在△ABE和△CAD中,
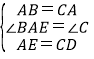 ,
,
∴△ABE≌△CAD(SAS);
(2)∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠ABE+∠BAP=∠CAD+∠BAP,
即∠BPQ=∠BAC=60°;
(3)∵BQ⊥AD,
∴∠BQP=90°,
∴∠PBQ=30°,
∴BP=2PQ=12,
∴BE=BP+PE=12+2=14
-
科目: 来源: 题型:
查看答案和解析>>【题目】疫情期间,为减少交叉感染,催生了以智能技术为支撑的无接触服务.某快递公司准备购进
 ,
, 两种型号的智能机器人送快递.经市场调査发现,
两种型号的智能机器人送快递.经市场调査发现, 型号机器人的单价比
型号机器人的单价比 型号机器人贵600元,3台
型号机器人贵600元,3台 型号机器人比2台
型号机器人比2台 型号机器人贵1200元.
型号机器人贵1200元.(1)求
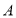 ,
, 两种型号机器人的单价各是多少元?
两种型号机器人的单价各是多少元?(2)若该快递公司准备用不超过132000元购进
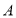 ,
, 两种型号机器人共50台,请问该快递公司最多可购进
两种型号机器人共50台,请问该快递公司最多可购进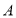 型号机器人多少台?
型号机器人多少台? -
科目: 来源: 题型:
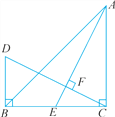
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作AE 的垂线CF,垂足为F,过点B作BD⊥BC,交CF的延长线于点D.
(1)求证:AE=CD.
(2)若AC=12 cm,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】具备下列条件的三角形中,不是直角三角形的是( )
A. ∠A+∠B=∠C B. ∠B=∠C=
 ∠A
∠AC. ∠A=90°-∠B D. ∠A-∠B=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张两边分别平行的纸条折成如图所示,EF为折痕,ED交BF于点G,且∠EFB=48°,则下列结论: ①∠DEF=48°;②∠AED=84°;③∠BFC=84°;④∠DGF=96°,其中正确的个数有( )
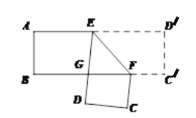
A. 4个B. 3个C. 2个D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D.

(1)求证:△ACB∽△ADE;
(2)求AD的长度.
相关试题

