【题目】如图,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式及顶点Q的坐标;
(2)在抛物线上是否存在点P,使△BPC的内心在y轴上,若存在,求出点P的坐标,若不存在写出理由;
(3)直线y=kx-6与y轴交于点N,与直线AC的交点为M,当△MNC与△AOC相似时,求点M坐标。

参考答案:
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+4,Q
x+4,Q![]() (2)(﹣5,﹣16)(3)①
(2)(﹣5,﹣16)(3)①![]() ②
②![]()
【解析】试题分析:(1)利用一次函数的解析式求出点A、C的坐标,然后再利用B点坐标即可求出二次函数的解析式;(2)由于M在抛物线F1上,所以可设M(a,-![]() ),然后分别计算S四边形MAOC和S△BOC,过点M作MP⊥x轴于点P,则S四边形MAOC的值等于△APM的面积与梯形POCM的面积之和.(3)由于没有说明点P的具体位置,所以需要将点P的位置进行分类讨论,当点P在A′的右边时,此情况是不存在;当点P在A′的左边时,此时∠DA′P=∠CAB′,若以A′、D、P为顶点的三角形与△AB′C相似,则分为以下两种情况进行讨论:①
),然后分别计算S四边形MAOC和S△BOC,过点M作MP⊥x轴于点P,则S四边形MAOC的值等于△APM的面积与梯形POCM的面积之和.(3)由于没有说明点P的具体位置,所以需要将点P的位置进行分类讨论,当点P在A′的右边时,此情况是不存在;当点P在A′的左边时,此时∠DA′P=∠CAB′,若以A′、D、P为顶点的三角形与△AB′C相似,则分为以下两种情况进行讨论:①![]() =
=![]() ;②
;②![]() =
=![]() .
.
试题解析:(1)令y=0代入y=![]() x+4,
x+4,
∴x=﹣3,A(﹣3,0),
令x=0,代入y=![]() x+4,∴y=4,∴C(0,4),
x+4,∴y=4,∴C(0,4),
设抛物线F1的解析式为:y=a(x+3)(x﹣1),
把C(0,4)代入上式得,a=﹣![]() ,
,
∴y=﹣![]() x2﹣
x2﹣![]() x+4,Q
x+4,Q![]()
(2)∵点B的坐标为(1,0),
取点B关于y轴的对称点B′(﹣1,0),连接CB′,
则∠BCO=∠B′CO,
∴△BPC的内心在y轴上,直线B′C的解析式为y=4x+4,
联立, ![]()
∴点P的坐标为(﹣5,﹣16);

N(0,-6),直线AC的表达式为![]() ,
,
当△MNC∽△AOC时,①∠CMN为直角
设 ![]() ,根据勾股定理可得
,根据勾股定理可得![]()
②当∠CNM为直角时,MN∥x轴,∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和为1800°,则这个多边形的边数为( )
A. 12 B. 11 C. 10 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a-3b=8,那么代数式5+2a-6b的值是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 3x+6y=9xyB. ﹣a2﹣a2=0
C. 2(3x+2)=6x+2D. ﹣(3x﹣2y)=﹣3x+2y
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于E交AB的延长线于点F,

(1)求证:EF是⊙O的切线;
(2)若AE=6,FB=4,求⊙O的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】折叠矩形ABCD,使它的顶点D落在BC边上的F处,如图,AB=6,AD=10,那么CE的长为 .
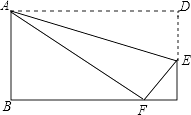
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年里约奥运会后,同学们参与体育锻炼的热情高涨,为了解他们平均每周的锻炼时间,小明同学在校内随机调查了50名同学,统计并制作了如下频数分布表和扇形统计图。根据上述信息解答下列问题:

(1)m=____,n=____;
(2)在扇形统计图中,D组所占圆心角的度数是____;
(3)全校共有3000名学生,该校平均每周体育锻炼时间不少于6小时的学生约有多少名?
相关试题

