搜索
【题目】甲、乙两人参加某体育项目训练，为了便于研究，把最后5次的训练成绩分别用实线和虚线连接起来，如图，下面的结论错误的是（ ）
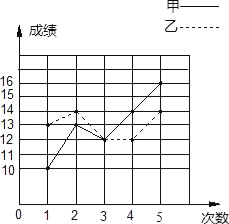
A. 乙的第2次成绩与第5次成绩相同
B. 第3次测试，甲的成绩与乙的成绩相同
C. 第4次测试，甲的成绩比乙的成绩多2分
D. 在5次测试中，甲的成绩都比乙的成绩高
参考答案：
【答案】D
【解析】
根据折线统计图中的信息即可作出判断．
A. 从统计图可以看出，乙的第2次成绩与第5次成绩相同，故A正确
B. 从统计图可以看出，第3次测试，甲的成绩与乙的成绩相同，故B正确
C. 从统计图可以看出，第4次测试，甲的成绩比乙的成绩多2分，故C正确
D. 从统计图可以看出， 5次测试中，甲的成绩为10+13+12+14+16=65,乙的成绩为13+14+12+12+14=65,甲乙成绩相同，故D错误.
故答案选：D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠ABM=45°，AM⊥BM，垂足为M，点C是BM延长线上一点，连接AC．
（1）如图1，若AB=3
，BC=5，求AC的长；
（2）如图2，点D是线段AM上一点，MD=MC，点E是△ABC外一点，EC=AC，连接ED并延长交BC于点F，且点F是线段BC的中点，求证：∠BDF=∠CEF． -
科目： 来源： 题型：
查看答案和解析>>【题目】(1)已知图1将线段AB向右平移1个单位长度,图2是将线段AB折一下再向右平移1个单位长度,请在图3中画出一条有两个折点的折线向右平移1个单位长度的图形；
(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩下部分的面积；
(3)如图4，在宽为10 m,长为40 m的长方形菜地上有一条弯曲的小路,小路宽度为1 m,求这块菜地的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】对任意一个三位数n，如果n满足各个数位上的数字互不相同，且都不为零，那么称这个数为“相异数”，将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与111的商记为F（n）．例如n=123，对调百位与十位上的数字得到213，对调百位与个位上的数字得到321，对调十位与个位上的数字得到132，这三个新三位数的和为213+321+132=666，666÷111=6，所以F（123）=6．
（1）计算：F（243），F（617）；
（2）若s，t都是“相异数”，其中s=100x+32，t=150+y（1≤x≤9，1≤y≤9，x，y都是正整数），规定：k=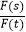
，当F（s）+F（t）=18时，求k的最大值． -
科目： 来源： 题型：
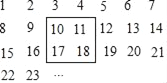
查看答案和解析>>【题目】把正整数1，2，3，4，…排列成如图所示的一个表．
（1）用一正方形在表中随意框住4个数，把其中最大的数记为x，另三个数用含x的式子表示出来，从大到小依次是 ， ， ；
（2）在（1）的前提下，当被框住的4个数之和等于984时，x位于该表的第几行第几列？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，抛物线y=
x2﹣ 
x﹣ 
与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，对称轴与x轴交于点D，点E（4，n）在抛物线上．
（1）求直线AE的解析式；
（2）点P为直线CE下方抛物线上的一点，连接PC，PE．当△PCE的面积最大时，连接CD，CB，点K是线段CB的中点，点M是CP上的一点，点N是CD上的一点，求KM+MN+NK的最小值；
（3）点G是线段CE的中点，将抛物线y= x2﹣ x﹣ 沿x轴正方向平移得到新抛物线y′，y′经过点D，y′的顶点为点F．在新抛物线y′的对称轴上，是否存在一点Q，使得△FGQ为等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏，下列命题中错误的是（ ）
A.红红不是胜就是输，所以红红胜的概率为
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为
D.娜娜胜的概率和两人出相同手势的概率一样
相关试题
