搜索
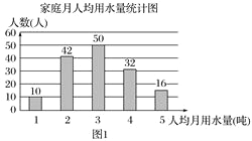
【题目】2010年春季以来，我国西南地区遭受了严重的旱情，某校学生会自发组织了“保护水资源从我做起”的活动．同学们采取问卷调查的方式，随机调查了本校150名同学家庭月人均用水量和节水措施情况．以下是根据调查结果作出的统计图的一部分．
请根据以上信息解答问题：
(1)补全图1和图2；
(2)如果全校学生家庭总人数约为3 000人，根据这150名同学家庭月人均用水量，估计全校学生家庭月用水总量．
参考答案：
【答案】（1）补图见解析；（2）9040吨.
【解析】
（1）用水为3吨的家庭数=总数－其它用水量的家庭数，淘米水浇花占的比例=总数1﹣安装节水设备所占比例﹣洗衣用水冲马桶所占比例－其他所占比例；
（2）全校学生家庭月用水总量=全校学生家庭总数×150户用水的平均用水量．
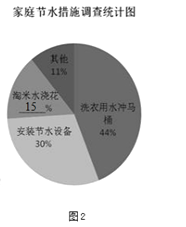
（1）用水为3吨的家庭数=150－10－42－32－16=50，淘米水浇花占的比例=1－30%－44%－11%=15%．补全图形如下：
（2）全体学生家庭月人均用水量为
9040（吨）．
答：全校学生家庭月用水量约为9040吨．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形OABC是矩形，ADEF是正方形，点A、D在x轴的正半轴上，点C在y轴的正半轴上，点F在AB上，点B、E在反比例函数y=
的图象上，OA=1，OC=6，则正方形ADEF的边长为 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知线段AB=16cm，点C为线段AB上的一个动点，点D、E分别是AC和BC的中点．
（1）若点C恰为AB的中点，求DE的长；
（2）若AC=6cm，求DE的长；
（3）试说明不论AC取何值（不超过16cm），DE的长不变；
（4）知识迁移：如图2，已知∠AOB=130°，过角的内部任一点C画射线OC，若OD、OE分别平分∠AOC和∠BOC，试说明∠DOE=65°与射线OC的位置无关．
-
科目： 来源： 题型：
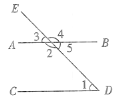
查看答案和解析>>【题目】如图,直线AB，CD被DE所截，则∠1和 是同位角，∠1和 是内错角，∠1和 是同旁内角；
(2)在(1)中，如果∠5=∠1,那么∠1=∠3的推理过程如下,请在括号内注明理由：
因为∠5=∠1( )，
∠5=∠3( )，
所以∠1=∠3( ).
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学为调查本校学生平均每天完成作业所用时间的情况，随机调查了50名同学，如图是根据调查所得数据绘制的统计图的一部分．
请根据以上信息，解答下列问题：
(1)将统计图补充完整；
(2)若该校共有1 800名学生，根据以上调查结果估计该校全体学生平均每天完成作业所用总时间．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=1，且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①可得到点P1 ， 此时AP1=
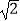；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2 ， 此时AP2=1+ 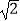；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3 ， 此时AP3=2+ 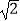；…，按此规律继续旋转，直至得到点P2015为止．则AP2015= ．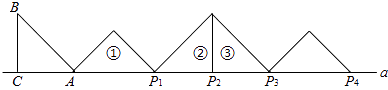 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC 中，点 D，E 分别在边 AC，AB 上，BD 与 CE 交于点 O，给出下列三个条件：①∠EBO＝∠DCO；②BE＝CD；③OB＝OC．
(1)上述三个条件中，由哪两个条件可以判定△ABC 是等腰三角形？(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形，写出证明过程．
相关试题
