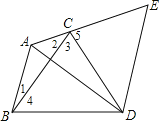
【题目】已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.

参考答案:
【答案】(1)60°;(2)5.
【解析】
试题分析:根据等边三角形的性质由△BCD为等边三角形得到∠3=∠4=60°,DC=DB,再根据旋转的性质得到∠5=∠1+∠4=∠1+60°,则∠2+∠3+∠5=∠2+∠1+120°,再根据三角形内角和定理得到
∠1+∠2=180°-∠BAC=60°,于是∠2+∠3+∠5=60°+120°=180°,即可得到点A、C、E在一条直线上;
由于点A、C、E在一条直线上,△ABD绕着点D按顺时针方向旋转60°后得到△ECD,则∠ADE=60°,DA=DE,得到△ADE为等边三角形,则∠DAE=60°,然后利用∠BAD=∠BAC-∠DAE计算即可;
由于点A、C、E在一条直线上,则AE=AC+CE,根据旋转的性质得到CE=AB,则AE=AC+AB=2+3=5,而△ADE为等边三角形,则AD=AE=5.
试题解析:∵△BCD为等边三角形,∴∠3=∠4=60°,DC=DB,∵△ABD绕着点D按顺时针方向旋转60°后得到△ECD,∴∠5=∠1+∠4=∠1+60°,∴∠2+∠3+∠5=∠2+∠1+120°,∵∠BAC=120°,
∴∠1+∠2=180°-∠BAC=60°,∴∠2+∠3+∠5=60°+120°=180°,∴点A、C、E在一条直线上;∵点A、C、E在一条直线上,而△ABD绕着点D按顺时针方向旋转60°后得到△ECD,∴∠ADE=60°,DA=DE,
∴△ADE为等边三角形,∴∠DAE=60°,∴∠BAD=∠BAC-∠DAE=120°-60°=60°;
∵点A、C、E在一条直线上,∴AE=AC+CE,∵△ABD绕着点D按顺时针方向旋转60°后得到△ECD,
∴CE=AB,∴AE=AC+AB=2+3=5,∵△ADE为等边三角形,∴AD=AE=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的∠BAD=∠C=90,AB=AD,AE⊥BC于E,
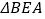 旋转后能与
旋转后能与 重合.
重合.(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)若AE=5㎝,求四边形AECF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出
(1)如图①,已知△ABC,请画出△ABC关于直线AC对称的三角形.
(2)问题探究
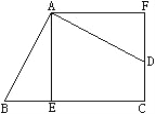
如图②,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
(3)如图③,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG= 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由.
米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由.
-
科目: 来源: 题型:
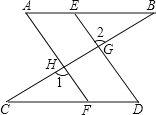
查看答案和解析>>【题目】如图,已知:E、F分别是AB和CD上的点,DE、AF分别交BC于点G、H, AB∥CD,∠A=∠D,试说明:(1)AF∥ED;(2)∠BED=∠A;(3) ∠1=∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.


-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式中,含有因式
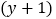 的多项式是( )
的多项式是( )A.
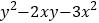 B.
B. 
C.
 D.
D. 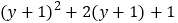
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校七年级三班有50名学生,现对学生最喜欢的球类运动进行了调查,根据调查的结果制作了扇形统计图,如图所示.根据扇形统计图中提供的信息,给出以下结论:
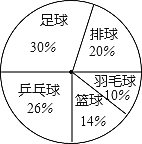
①最喜欢足球的人数最多,达到了15人;
②最喜欢羽毛球的人数最少,只有5人;
③最喜欢排球的人数比最喜欢乒乓球的人数少3人;
④最喜欢乒乓球的人数比最喜欢篮球的人数多6人。
其中正确的结论有
A. 1个B. 2个C. 3个D. 4个
相关试题

