【题目】阅读材料:设一元二次方程![]() (a≠0)的两根为
(a≠0)的两根为![]() , 则两根与方程的系数之间有如下关系:
, 则两根与方程的系数之间有如下关系:![]() ,
, ![]() .根据该材料完成下列填空:
.根据该材料完成下列填空:
已知m,n是方程![]() 的两根,则
的两根,则
(1)![]() =____, mn=____;
=____, mn=____;
(2)![]() =_________.
=_________.
参考答案:
【答案】(1)2012 ,2013;(2)2.
【解析】
(1)根据根与系数的关系即可得出m+n=2012、mn=2013,此题得解;
(2)由m,n是方程x2-2012x+2013=0的两根,即可得出m2-2012m+2013=0、n2-2012n+2013=0,(m2-2013m+2014)(n2-2013n+2014)即可变形为1+mn-(m+n),代入数据即可得出结论.
(1)∵m,n是方程x2-2012x+2013=0的两根,
∴m+n=2012,mn=2013,
(2) ∵m,n是方程x2-2012x+2013=0的两根,
∴m2-2012m+2013=0, n2-2012n+2013=0,
∴m2-2013m+2014=m2-2012m+2013+1-m=0+1-m=1-m;
n2-2013n+2014=n2-2012n+2013+1-n=0+1-n=1-n;
∴(m2-2013m+2014)(n2-2013n+2014)
=(1-m)(1-n)
=1-(m+n)+mn
=1-2012+2013
=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校,以下是他本次上学所用的时间与路程的关系示意图
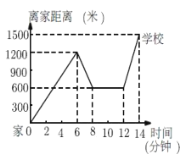
根据图中提供的信息回答下列问题
(1)小明家到学校的路程是__________米,从家到学校一共用了__________分钟.
(2)小明在书店停留了__________分钟.
(3)本次上学途中,小明12到14分行驶了__________米.12到14分的速度__________米/分.
(4)在整个上学的途中__________(哪个时间段)速度最快.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图,若双曲线
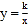 (k>0)与它的其中一条对称轴y=x相交于两点A,B,则线段AB的长称为双曲线
(k>0)与它的其中一条对称轴y=x相交于两点A,B,则线段AB的长称为双曲线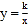 (k>0)的对径.
(k>0)的对径.
(1)求双曲线
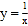 的对径;
的对径;(2)若某双曲线
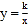 (k>0)的对径是
(k>0)的对径是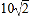 .求k的值.
.求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲16分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

-
科目: 来源: 题型:
查看答案和解析>>【题目】黄岩某校搬迁后,需要增加教师和学生的寝室数量,寝室有三类,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2018年学校寝室数为64个,以后逐年增加,预计2020年寝室数达到121个,求2018至2020年寝室数量的年平均增长率;
(2)若三类不同的寝室的总数为121个,则最多可供多少师生住宿?
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按
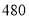 元销售时,每天可销售
元销售时,每天可销售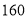 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出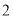 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为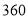 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润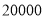 元?
元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图抛物线y=ax2+2交x轴于点A(﹣2,0)、B,交y轴于点C;
(1)求抛物线的解析式;
(2)点P从点A出发,以1个单位/秒的速度向终点B运动,同时点Q从点C出发,以相同的速度沿y轴正方向向上运动,运动的时间为t秒,当点P到达点B时,点Q也停止运动,设△PQC的面积为S,求S与t间的函数关系式并直接写出t的取值范围;
(3)在(2)的条件下,当点P在线段OB上时,设PQ交直线AC于点G,过P作PE⊥AC于点E,求EG的长.
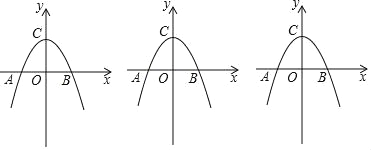
相关试题

