【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲16分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

参考答案:
【答案】(1)第30分钟注意力更集中.(2)老师能在学生注意力达到所需的状态下讲解完这道题目.
【解析】试题分析:(1)先用代定系数法分别求出AB和CD的函数表达式,再分别求第五分钟和第三十分钟的注意力指数,最后比较判断;
(2)分别求出注意力指数为36时的两个时间,再将两时间之差和19比较,大于19则能讲完,否则不能.
试题解析:(1)设线段AB所在的直线的解析式为y1=k1x+20,
把B(10,40)代入得,k1=2,∴y1=2x+20.设C、D所在双曲线的解析式为y2=![]() ,
,
把C(25,40)代入得,k2=1000,∴![]()
当x1=5时,y1=2×5+20=30,当![]() ,∴y1<y2
,∴y1<y2
∴第30分钟注意力更集中.
(2)令y1=36,∴36=2x+20,∴x1=8令y2=36,∴![]() ,∴
,∴![]()
∵27.8﹣8=19.8>19,
∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c<0的解集;
(3)若方程ax2+bx+c+k=0有两个不相等的实数根,求k的取值范围.
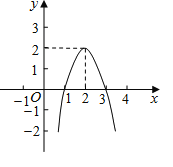
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小明全家登山旅游,走一条12千米的山路,又沿原路返回,上山的时候速度是每小时2千米,下山的时候速度是每小时6千米,他们上山、下山的平均速度是每小时_____千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是外角和的2倍,则这个多边形是( )
A.四边形
B.五边形
C.六边形
D.八边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算结果正确的是( )
A. a5+a5=2a10B. (x3)3=x6C. x5x=x6D. (ab2)3=ab6
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线
 (a、b、c是常数,
(a、b、c是常数,  )与直线
)与直线 都经过
都经过 轴上的一点P,且抛物线L的顶点Q在直线
轴上的一点P,且抛物线L的顶点Q在直线 上,则称此直线
上,则称此直线 与该抛物线L具有“一带一路”关系,此时,直线
与该抛物线L具有“一带一路”关系,此时,直线 叫做抛物线L的“带线”,抛物线L叫做直线
叫做抛物线L的“带线”,抛物线L叫做直线 的“路线”.
的“路线”.(1)若直线
 与抛物线
与抛物线 具有“一带一路”关系,求m、n的值.
具有“一带一路”关系,求m、n的值.(2)若某“路线”L的顶点在反比例函数
 的图象上,它的“带线” 的解析式为
的图象上,它的“带线” 的解析式为 ,求此路的解析式.
,求此路的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面每组数分别是三根小木棒的长度,用它们不能摆成一个三角形的是( )
A. 5cm,10cm,5cmB. 7cm,8cm,9cm
C. 3cm,4cm,5cmD. 6cm,20cm,20cm
相关试题

