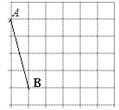
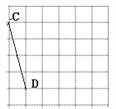
【题目】如图网格中每个小正方形的边长均为1,线段AB、CD的端点都在小正方形的顶点上.
(1)图(1)中,画一个以线段AB一边的四边形ABEF,且四边形ABEF是面积为7的中心对称图形,点E、F都在小正方形的顶点上,并直接写出线段BE的长;
(2)在图(2)中,画一个以线段CD为斜边直角三角形CDG,且△CDG的面积是2,点G在小方形的顶点上。
参考答案:
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)根据平行四边形两组对边相等画图,还要注意到所画的平行四边形的面积为7;
(2)根据直角三角形,且△CDG的面积是2,利用网格画一两直角边为1和4的直角三角形的斜边即可.
试题解析:解:(1)如图1所示:四边形ABEF即为所求:
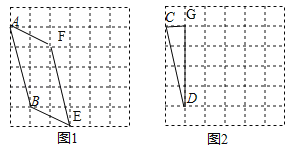
BE=![]() ;
;
(2)如图2所示:△CDG即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,BE⊥CE,垂足是E,BE交AC于点D,F是BE上一点,AF⊥AE,且C是线段AF的垂直平分线上的点,AF=2
 ,则DF=______.
,则DF=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解(solution).已知:关于
 的方程
的方程 .
.(1)若
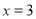 是方程
是方程 的解,求
的解,求 的值;
的值;(2)若关于
 的方程
的方程 的解比方程
的解比方程 的解大6,求
的解大6,求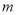 的值;
的值;(3)若关于
 的方程
的方程 与
与 均无解,求代数式
均无解,求代数式 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC,∠C=90°,AD平分∠BAC交CB于点D,过点D作DE⊥AB,垂足恰好是边AB的中点E.若AD=3cm,则BE的长为( )
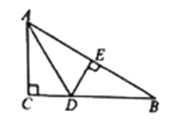
A.
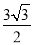 cmB. 4cmC. 3
cmB. 4cmC. 3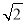 cmD. 6cm
cmD. 6cm -
科目: 来源: 题型:
查看答案和解析>>【题目】从A,B两题中任选一题作答:
A.如图,在ΔABC中,分别以点A,B为圆心,大于
 AB的长为半径画弧,两弧交与点M,N,作直线MN交AB于点E,交BC于点F,连接AF。若AF=6,FC=4,连接点E和AC的中点G,则EG的长为__.
AB的长为半径画弧,两弧交与点M,N,作直线MN交AB于点E,交BC于点F,连接AF。若AF=6,FC=4,连接点E和AC的中点G,则EG的长为__.
B.如图,在ΔABC中,AB=2,∠BAC=60°,点D是边BC的中点,点E在边AC上运动,当DE平分ΔABC的周长时,DE的长为__.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课上,老师出了这样一道题:甲、乙两地相距1400km,乘高铁列车从甲地到乙地比乘特快列车少用9h,已知高铁列车的平均行驶速度是特快列车的2.8倍。求高铁列车从甲地到乙地的时间.老师要求同学先用列表方式分析再解答.下面是两个小组分析时所列的表格:
小组甲:设特快列车的平均速度为xkm/h.

小组乙:高铁列车从甲地到乙地的时间为yh

(1)根据题意,填写表格中空缺的量;(2)结合表格,选择一种方法进行解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:

(1)本次被调查的学生有 名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
相关试题

