【题目】如图1,点I是△ABC的内心,AI的延长线交△ABC的外接圆⊙O于点D.

(1)求证:DB=DC=DI;
(2)若AB是⊙O的直径,OI⊥AD,求tan![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)要证明ID=BD=DC,只要求得∠BID=∠IBD,再根据角平分线的性质即可得到结论;
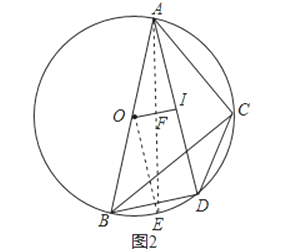
(2)由AB是⊙O的直径,得到BD⊥AD,由于OI⊥AD,得到OI∥BD,于是求得AD=2BD,BD=2OI,设OI=x,则BD=AI=2x,AD=4x,得到AB= ![]() ,如图2,过O作OE⊥BD交⊙O于E,连接AE交OI于F,则OE∥AI,得到比例式代入求得IF=
,如图2,过O作OE⊥BD交⊙O于E,连接AE交OI于F,则OE∥AI,得到比例式代入求得IF= ![]() ,即可得到结果.
,即可得到结果.
试题解析:(1)证明:∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∴∠BID=∠ABI+∠BAD,
∴∠ABI=∠CBI,∠BAD=∠CAD=∠CBD,
∵∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴ID=BD,
∵∠BAD=∠CAD,
∴![]() ,
,
∴CD=BD,
∴DB=DC=DI;
(2)∵AB是⊙O的直径,
∴BD⊥AD,OI⊥AD,
∴OI∥BD,
∵OA=OB,
∴AI=DI,
由(1)知ID=BD,
∴AD=2BD,BD=2OI,
设OI=x,则BD=AI=2x,AD=4x,
∴AB= ![]() ,
,
如图2,过O作OE⊥BD交⊙O于E,连接AE交OI于F,则OE∥AI,
∴![]() ,
,
即![]() ,
,
∴IF= ![]() ,
,
∵OE⊥BD,
∴![]() ,
,
∴∠DAE=![]() ∠BAD=
∠BAD=![]() ∠CAD,
∠CAD,
∴tan∠DAE= tan![]() =
=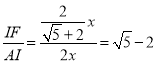 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】人在运动时每分钟心跳的次数通常和人的年龄有关,如果用
 表示一个人的年龄,用
表示一个人的年龄,用 表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,那么
表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,那么 .
. 正常情况下,在运动时一个
正常情况下,在运动时一个 岁的人所能承受的每分钟心跳的最高次数是多少?
岁的人所能承受的每分钟心跳的最高次数是多少? 一个
一个 岁的人运动时
岁的人运动时 秒心跳的次数为
秒心跳的次数为 ,请问他有危险吗?为什么?
,请问他有危险吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点P的横坐标为x,纵坐标为2x,满足这样条件的点称为“关系点”.
(1)在点A(1,2)、B(2,1)、M(
 ,1)、N(1,
,1)、N(1,  )中,是“关系点”的为 ;
)中,是“关系点”的为 ;(2)⊙O的半径为1,若在⊙O上存在“关系点”P,求点P坐标;
(3)点C的坐标为(3,0),若在⊙C上有且只有一个“关系点”P,且“关系点”P的横坐标满足-2≤x≤2.请直接写出⊙C的半径r的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元,已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次采购的数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.为出口需要,所有采购的大蒜必须在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半.为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以3cm/s的速度向A点运动.设运动时间为x(s).

(1)当x为何值时,PQ∥BC;
(2)当△APQ与△CQB相似时,AP的长为________.;
(3)当S△BCQ:S△ABC=1:3,求S△APQ:S△ABQ的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.

相关试题

