【题目】在平面直角坐标系xOy中,点P的横坐标为x,纵坐标为2x,满足这样条件的点称为“关系点”.
(1)在点A(1,2)、B(2,1)、M(![]() ,1)、N(1,
,1)、N(1, ![]() )中,是“关系点”的为 ;
)中,是“关系点”的为 ;
(2)⊙O的半径为1,若在⊙O上存在“关系点”P,求点P坐标;
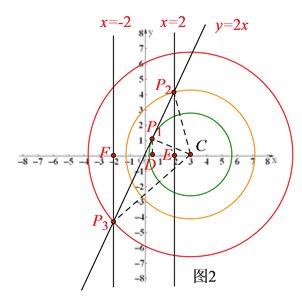
(3)点C的坐标为(3,0),若在⊙C上有且只有一个“关系点”P,且“关系点”P的横坐标满足-2≤x≤2.请直接写出⊙C的半径r的取值范围.

参考答案:
【答案】(1)A、M;(2)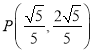 或
或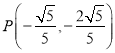 ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题分析:
(1)由“关系点”的定义可知,关系点的纵坐标等于横坐标的2倍,由此可知四个点中A点和M点是“关系点”;
(2)由题意按要求作半径为1的⊙O,如图1,在⊙O上取点P,根据关系点的定义设点P的坐标为(x,2x),过点P作PG⊥x轴于点G,在Rt△OPG中,由勾股定理建立方程,解方程求得x的值,即可得到点P的坐标;
(3)“关系点”P的横坐标满足-2≤x≤2,且⊙C上有且只有一个“关系点”P,故结合图2分以下两种情况讨论可得本题答案:①当⊙C和直线![]() 相切于点P1时,⊙C上有且只有一个“关系点”;②设点P2的坐标为(2,4),点P3的坐标为(-2,-4),连接CP2,CP3,当CP2<r<CP3时,⊙C上有且只有一个“关系点”;综合①②即可得到本题答案.
相切于点P1时,⊙C上有且只有一个“关系点”;②设点P2的坐标为(2,4),点P3的坐标为(-2,-4),连接CP2,CP3,当CP2<r<CP3时,⊙C上有且只有一个“关系点”;综合①②即可得到本题答案.
试题解析:
(1)由“关系点”的定义可知,“关系点”的纵坐标等于横坐标的2倍,由此可知四个点中点A、M是“关系点”;.
(2)由题意按要求作半径为1的⊙O,如图1,在⊙O上取点P,过点P作PG⊥x轴于点G,由题意可设P(x,2x),
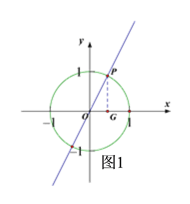
∵在Rt△OPG中,OG2+PG2=OP2 ,
∴x2+4x2=1,
∴5x2=1,
∴x2=![]() ,
,
∴x=![]() ,
,
∴P 或P
或P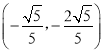 ;
;
(3)由“关系点”的定义可知,所有的关系点都在直线![]() 上;
上;
∵“关系点”P的横坐标满足-2≤x≤2,且⊙C上有且只有一个“关系点”P,
∴①当⊙C和直线![]() 相切于点P1时,⊙C上有且只有一个“关系点”;②设点P2的坐标为(2,4),点P3的坐标为(-2,-4),连接CP2,CP3,当CP2<r<CP3时,⊙C上有且只有一个“关系点”;
相切于点P1时,⊙C上有且只有一个“关系点”;②设点P2的坐标为(2,4),点P3的坐标为(-2,-4),连接CP2,CP3,当CP2<r<CP3时,⊙C上有且只有一个“关系点”;
①如图2,当⊙C和直线![]() 相切于点P1时,此时⊙C上有且只有一个“关系点”,
相切于点P1时,此时⊙C上有且只有一个“关系点”,
过点P1作P1D⊥x轴于点D,则OD=x,P1D=2x,OP1= ![]() ,
,
∴sin∠P1OD=![]() ,
,
∴此时⊙C的半径![]() =OC×sin∠P1OD=
=OC×sin∠P1OD=![]() ;
;
②如图2,当x=2时,点P2的坐标为(2,4),连接CP2,在Rt△CEP2中,由勾股定理可得CP2=![]() ;
;
当x=-2时,点P3的坐标为(-2,-4),连接CP3,在Rt△CFP3中,由勾股定理可得CP3=![]() ;
;
∴当![]() 时,在
时,在![]() 的范围内,⊙C与直线
的范围内,⊙C与直线![]() 只有一个交点.
只有一个交点.
综上所述,点C的坐标为(3,0),若在⊙C上有且只有一个“关系点”P,且“关系点”P的横坐标满足-2≤x≤2时,⊙C的半径![]() 的取值为:
的取值为: ![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线
 :
:  与抛物线
与抛物线 相交于点A(
相交于点A( ,7).
,7). (1)求m,n的值;
(2)过点A作AB∥x轴交抛物线于点B,设抛物线与x轴交于点C、D(点C在点D的左侧),求△BCD的面积;
(3)点E(t,0)为x轴上一个动点,过点E作平行于y轴的直线与直线
 和抛物线分别交于点P、Q.当点P在点Q上方时,求线段PQ的最大值.
和抛物线分别交于点P、Q.当点P在点Q上方时,求线段PQ的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,AB=AC,将线段BA绕点B顺时针旋转到BD,使BD⊥AC于H,连结AD并延长交BC的延长线于点P.
(1)依题意补全图形;
(2)若∠BAC=2α,求∠BDA的大小(用含α的式子表示);
(3)小明作了点D关于直线BC的对称点点E,从而用等式表示线段DP与BC之间的数量关系.请你用小明的思路补全图形并证明线段DP与BC之间的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】人在运动时每分钟心跳的次数通常和人的年龄有关,如果用
 表示一个人的年龄,用
表示一个人的年龄,用 表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,那么
表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,那么 .
. 正常情况下,在运动时一个
正常情况下,在运动时一个 岁的人所能承受的每分钟心跳的最高次数是多少?
岁的人所能承受的每分钟心跳的最高次数是多少? 一个
一个 岁的人运动时
岁的人运动时 秒心跳的次数为
秒心跳的次数为 ,请问他有危险吗?为什么?
,请问他有危险吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点I是△ABC的内心,AI的延长线交△ABC的外接圆⊙O于点D.

(1)求证:DB=DC=DI;
(2)若AB是⊙O的直径,OI⊥AD,求tan
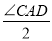 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元,已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次采购的数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.为出口需要,所有采购的大蒜必须在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半.为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少?
相关试题

