【题目】结合数轴与绝对值的知识回答下列问题:
(1)探究:
①数轴上表示5和2的两点之间的距离是多少.
②数轴上表示﹣2和﹣6的两点之间的距离是多少.
③数轴上表示﹣4和3的两点之间的距离是多少.
(2)归纳:
一般的,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.
(3)应用:
①如果表示数a和3的两点之间的距离是7,则可记为:|a﹣3|=7,求a的值.
②若数轴上表示数a的点位于﹣4与3之间,求|a+4|+|a﹣3|的值.
![]()
③当a取何值时,|a+4|+|a﹣1|+|a﹣3|的值最小,最小值是多少?请说明理由.
![]()
(4)拓展:某一直线沿街有2014户居民(相邻两户居民间隔相同):A1,A2,A3,A4,A5,…A2014,某餐饮公司想为这2014户居民提供早餐,决定在路旁建立一个快餐店P,点P选在什么线段上,才能使这2014户居民到点P的距离总和最小.
参考答案:
【答案】(1)探究:①3;②4;③7;(3)应用:①10或﹣4;②7;③7,理由是:a=1时,正好是3与﹣4两点间的距离;(4)A1007A1008这条线段上.
【解析】
(1)根据两点间的距离公式,可得答案;
(3)①根据两点间的距离公式,可得答案;
②根据线段上的点到线段两端点的距离的和最小,可得答案;
③根据线段上的点到线段两端点的距离的和最小,可得答案.
(4)点P选在A1007A1008这条线段上.
(1)探究:
①数轴上表示5和2的两点之间的距离是3.
②数轴上表示﹣2和﹣6的两点之间的距离是4.
③数轴上表示﹣4和3的两点之间的距离是7.
(3)应用:
①如果表示数a和3的两点之间的距离是7,则可记为:|a﹣3|=7, a=10或﹣4.
②若数轴上表示数a的点位于﹣4与3之间,
|a+4|+|a﹣3|=a+4+3﹣a=7;
③当a=1时,|a+4|+|a﹣1|+|a﹣3|取最小值,|a+4|+|a﹣1|+|a﹣3|最小=5+0+2=7,
理由是:a=1时,正好是3与﹣4两点间的距离.
(4)应用:点P选在A1007A1008这条线段上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠BAC=90°,AB=AC=2.以AC为一边,在△ABC外部作等腰直角三角形ACD,则线段BD的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当m为何值时,关于x的一元二次方程(2m+1)x2+4mx+2m﹣3=0.
(1)有两个不相等的实数根;
(2)有两个相等的实数根;
(3)没有实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式A=2x2+3xy+2y-1,B=x2-xy+x-

(1)求A2B;
(2)若A2B的值与x的取值无关,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2
 =(1+
=(1+ )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b =(m+n
=(m+n )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b =m2+2n2+2mn
=m2+2n2+2mn ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b 的式子化为平方式的方法。
的式子化为平方式的方法。
请我仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b =(m+n
=(m+n )2,用含m、n的式子分别表示a、b,得a=________, b=___________.
)2,用含m、n的式子分别表示a、b,得a=________, b=___________.(2)若a+4
 =(m+n
=(m+n )2,且a、m、n均为正整数,求a的值。
)2,且a、m、n均为正整数,求a的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商店购进一批滑板,每件进价为100元,售价为130元,每星期可卖出80件.商家决定降价促销,根据市场调查,每降价5元,每星期可多卖出20件.
(1)求商家降价前每星期的销售利润为多少元?
(2)降价后,商家要使每星期的销售利润最大,应将售价定为多少元?最大销售利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+2x+b的图象可能是( )
A.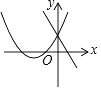
B.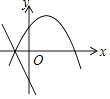
C.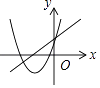
D.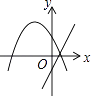
相关试题

