【题目】如图,矩形AOBC,点A、B分别在x、y轴上,对角线AB、OC交于点D,点C( ![]() ,1),点M是射线OC上一动点.
,1),点M是射线OC上一动点.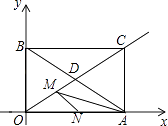
(1)求证:△ACD是等边三角形;
(2)若△OAM是等腰三角形,求点M的坐标;
(3)若N是OA上的动点,则MA+MN是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
参考答案:
【答案】
(1)证明:∵C( ![]() ,1),
,1),
∴AC=1,OA= ![]() ,
,
∴OC=2,
∴∠COA=30°,∠OCA=60°,
∵矩形AOBC,
∴AD=CD=OD
且∠OCA=60°
∴△ACD是等边三角形
(2)解:△OAM是等腰三角形,
当OM=MA时,此时点M与点D重合,
∵C( ![]() ,1),点D为OC中点,
,1),点D为OC中点,
∴M( ![]() ,
, ![]() ).
).
当OM1=OA时,做M1E⊥OA,垂足为E,如下图:
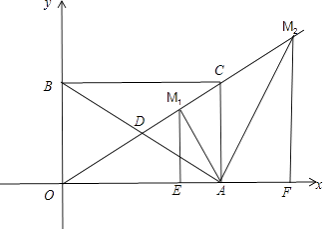
∴OM1=OA= ![]() ,
,
由(1)知∠M1OA=30°,
∴M1E= ![]() ,OE=
,OE= ![]() ,
,
∴M1( ![]() ,
, ![]() ).
).
当OA=OM2时,做M2F⊥OA,垂足为F,如上图:
AM2= ![]() ,
,
由(1)知∠COA=∠AM2O=30°,
∴∠M2AF=60°,
∴AF= ![]() ,M2F=
,M2F= ![]() ,
,
M2( ![]() ,
, ![]() ).
).
综上所述:点M坐标为M( ![]() ,
, ![]() )、(
)、( ![]() ,
, ![]() )、(
)、( ![]() ,
, ![]() )
)
(3)解:存在,做点A关于直线OC对称点为G,如下图:

则AG⊥OC,且∠GOA=60°OG=OA= ![]() ,
,
∴ON= ![]() ,GN=
,GN= ![]() ,
,
∵点A、G关于直线OC对称,
∴MG=MA,
∴MA+MN=MG+MN,
∵N是OA上的动点,
∴当GN⊥x轴时,MA+MN最小,
∴存在MA+MN存在最小值,最小值为 ![]() .
.
【解析】(1)利用点C(![]() 3,1),即可求出相应角度为30°,则∠OCA=60°,根据矩形的性质和直角三角形中斜边的中线等于斜边的一半,则得出了有两边相等,且有一个角是60°,即可证明三角形是等边三角形;
3,1),即可求出相应角度为30°,则∠OCA=60°,根据矩形的性质和直角三角形中斜边的中线等于斜边的一半,则得出了有两边相等,且有一个角是60°,即可证明三角形是等边三角形;
(2)此问结合了分类讨论的思想,由等腰三角形性质,对三角形OAM三边关系进行讨论,分别求出三种情况讨论,三种情况都是转换不同的边为底边,另外两边相等,然后根据不同的情况求出点M的坐标即可;
(3)根据最短路径探究,做点A关于直线OC对称点,利用对称性可以求出最小值。
【考点精析】本题主要考查了含30度角的直角三角形和矩形的性质的相关知识点,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(﹣1,0),点D的坐标为(1,6).
(1)求证:CD=CF;
(2)判断⊙P与y轴的位置关系,并说明理由;
(3)求直线BD的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】找规律:21-20=20 ;22-21=21 ;23-22=2 2;………利用你的发现,求20+21+22+23+…+22018+22019的值是( )
A. 22019 -1B. 22019 +1C. 22020 -1D. 22020 +1
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式m﹣ma2的结果是( )
A.m(1+a)(1﹣a)
B.m(1+a)2
C.mm(1﹣a)2
D.(1﹣a)(1+a) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的面积是( )
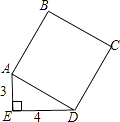
A.5
B.25
C.7
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.

(1)求DE的长;
(2)求△ADB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC⊥BD,且AC=8,BD=4,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,依此类推,这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为( )
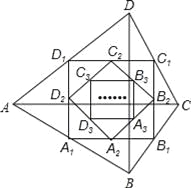
A.
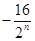 B.
B.  C.
C. 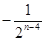 D. 不确定
D. 不确定
相关试题

