搜索
【题目】如图，正方形ABCD的面积是（ ）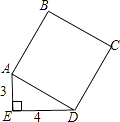
A.5
B.25
C.7
D.10
参考答案：
【答案】B
【解析】解：∵在R△tADE中，∠E=90°，AE=3，DE=4，
∴AD2=AE2+DE2=32+42=25，
∴正方形ABCD的面积=AD2=25．
所以答案是：B．
【考点精析】根据题目的已知条件，利用勾股定理的概念和正方形的性质的相关知识可以得到问题的答案，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】找规律：21－20＝20 ；22－21＝21 ；23－22＝2 2；………利用你的发现，求20＋21＋22＋23＋…＋22018＋22019的值是( )
A. 22019 -1B. 22019 +1C. 22020 -1D. 22020 +1
-
科目： 来源： 题型：
查看答案和解析>>【题目】分解因式m﹣ma2的结果是（ ）
A.m（1+a）（1﹣a）
B.m（1+a）2
C.mm（1﹣a）2
D.（1﹣a）（1+a） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形AOBC，点A、B分别在x、y轴上，对角线AB、OC交于点D，点C（
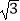，1），点M是射线OC上一动点．
（1）求证：△ACD是等边三角形；
（2）若△OAM是等腰三角形，求点M的坐标；
（3）若N是OA上的动点，则MA+MN是否存在最小值？若存在，请求出这个最小值；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，Rt△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于E，若AC=6，BC=8，CD=3．
（1）求DE的长；
（2）求△ADB的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，对角线AC⊥BD，且AC=8，BD=4，各边中点分别为A1、B1、C1、D1，顺次连接得到四边形A1B1C1D1，再取各边中点A2、B2、C2、D2，顺次连接得到四边形A2B2C2D2，…，依此类推，这样得到四边形AnBnCnDn，则四边形AnBnCnDn的面积为（ ）
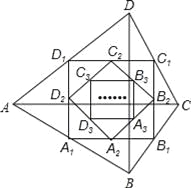
A.
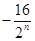B. 
C.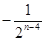 
D. 不确定 -
科目： 来源： 题型：
查看答案和解析>>【题目】（1）阅读以下内容：
已知实数x，y满足x+y=2，且
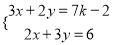求k的值．三位同学分别提出了以下三种不同的解题思路：
甲同学：先解关于x，y的方程组
，再求k的值．乙同学：先将方程组中的两个方程相加，再求k的值．
丙同学：先解方程组
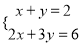，再求k的值．（2）你最欣赏（1）中的哪种思路？先根据你所选的思路解答此题，再对你选择的思路进行简要评价．
（评价参考建议：基于观察到题目的什么特征设计的相应思路，如何操作才能实现这些思路、运算的简洁性，以及你依此可以总结什么解题策略等等）
请先在以下相应方框内打勾，再解答相应题目．
相关试题
