【题目】如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(﹣1,0),点D的坐标为(1,6).
(1)求证:CD=CF;
(2)判断⊙P与y轴的位置关系,并说明理由;
(3)求直线BD的解析式.

参考答案:
【答案】(1)见解析;(2) ⊙P与y轴相切,理由见解析;(3) y=-![]() x+
x+![]()
【解析】试题分析: (1)证△COF≌△CHD可得CD=CF;
(2)连接PC,先由CD=CF、PD=PB知PC∥BF,结合BF⊥y轴知PC⊥y轴,即可得出结论;
(3)连接AD,证BD=BF可得AD=OH=6、OA=DH=1,设BD=x,由BD2=AB2+AD2得x=10,从而知B(9,0),待定系数法求解可得.
试题解析:
(1)如图,作DH⊥OE于点H,

∴∠DHC=∠FOC=90°,∠DCH=∠FCO,
∵D(1,6)、F(﹣1,0),
∴DH=OF=1,
在△COF和△CHD中,
∵ ,
,
∴△COF≌△CHD(AAS),
∴CD=CF;
(2)连接PC,
∵CD=CF、PD=PB,
∴PC为△BDF的中位线,
∴PC∥BF,
∵BF⊥y轴,
∴PC⊥y轴,
又PC为⊙P的半径,
∴⊙P与y轴相切;
(3)如图,连接AD,
由(2)知BF=2PC,
∵BD=2PC,
∴BD=BF,
∵BD是⊙P的直径,
∴∠DAB=90°,
∴AD=OH=6,OA=DH=1,
设BD=x,
则AB=x﹣2,
由BD2=AB2+AD2得x2=(x﹣2)2+62,
解得:x=10,
∴OB=OA+AB=1+8=9,即B(9,0),
设直线BD的解析式为y=kx+b,
把B(9,0)、D(1,6)代入得![]() ,
,
解得:![]() ,
,
∴直线BD的解析式为y=-![]() x+
x+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年元旦期间,地铁1号线日乘人数最高达到140000人次,数字140000用科学记数法可表示为( )
A.1.4×104
B.1.4×10﹣5
C.1.4×105
D.1.4×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,P是对角线BD上的点,点E在AB上,且PA=PE.

(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,试探究∠CPE与∠ABC之间的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x﹣2y=3,则代数式6﹣2x+4y的值为( )
A.0
B.﹣1
C.﹣3
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】找规律:21-20=20 ;22-21=21 ;23-22=2 2;………利用你的发现,求20+21+22+23+…+22018+22019的值是( )
A. 22019 -1B. 22019 +1C. 22020 -1D. 22020 +1
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式m﹣ma2的结果是( )
A.m(1+a)(1﹣a)
B.m(1+a)2
C.mm(1﹣a)2
D.(1﹣a)(1+a) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形AOBC,点A、B分别在x、y轴上,对角线AB、OC交于点D,点C(
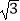 ,1),点M是射线OC上一动点.
,1),点M是射线OC上一动点.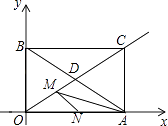
(1)求证:△ACD是等边三角形;
(2)若△OAM是等腰三角形,求点M的坐标;
(3)若N是OA上的动点,则MA+MN是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
相关试题

