【题目】(类比探究)如图1,线段AD,CB相交于点O,连接AB,DC,我们把形如图1的图形称之为“X型”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AE和CE相交于点E,并且与CB,AD分别相交于F,G,试解答下列问题:
(1)在图1中,请直接写出∠A,∠B,∠C,∠D之间的数量关系:____________;
(2)在图2中,共有______个“X型”;
(3)在图2中,若∠D=40°,∠B=30°,则∠AEC=_______;
(4)在图2中,若∠D=α,∠B=β,则∠AEC=__________.

参考答案:
【答案】(1)∠A+∠D=∠C+∠B;(2)6;(3)35°;(4)α+β.
【解析】
(1)根据三角形内角和定理即可得出∠A+∠B=∠C+∠D;
(2)根据“X型”的定义,仔细观察图形即可得出“X型”共有6个;
(3)先根据“X型”中的角的规律,可得∠BAE+∠B=∠E+∠ECB①,∠ECD+∠D=∠EAD+∠E②,再根据角平分线的定义,得出∠BAE=∠EAD,∠BCE=∠ECD,将①+②,可得2∠E=∠D+∠B,进而求出∠E的度数;
(4)同(3),根据“X型”中的角的规律及角平分线的定义,即可得出2∠AEC=α+β.
(1)∵∠A+∠B+∠AOB=∠C+∠D+∠DOC=180°,∠AOB=∠DOC,
∴∠A+∠B=∠C+∠D;
故答案为:∠A+∠D=∠C+∠B;
(2)①线段AD、CB相交于点O,形成“X型”;
②线段AG、CF相交于点O,形成“X型”;
③线段AD、CE相交于点G,形成“X型”;
④线段AD、CF相交于点O,形成“X型”;
⑤线段AE、CB相交于点F,形成“X型”;
⑥线段AG、CB相交于点O,形成“X型”;
故“X型”共有6个;
故答案为:6.
(3)∠BAE+∠B=∠E+∠ECB,①
∠ECD+∠D=∠EAD+∠E,②
∵∠DAB和∠BCD的平分线AE和CE相交于点E,
∴∠DAE=∠EAB,∠DCE=∠ECB,
①+②得:
∠BAE+∠B +∠ECD+∠D =∠E+∠ECB +∠EAD+∠E,
即2∠E=∠D+∠B,
又∵∠D=40°,∠B=30°,
∴2∠E=40°+30°=70°,
∴∠AEC=35°;
故答案为:35°;
(4)由(3)知:2∠E=∠D+∠B.
∵∠D=α,∠B=β,
∴2∠E=α+β.
故答案为:α+β.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 中,点
中,点 为直角坐标系的原点,
为直角坐标系的原点, 的坐标分别为
的坐标分别为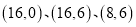 .点
.点 同时从原点出发,分别作匀速运动,点
同时从原点出发,分别作匀速运动,点 沿
沿 以每秒1个单位向终点
以每秒1个单位向终点 运动,点
运动,点 沿
沿 以每秒2个单位向终点
以每秒2个单位向终点 运动.当这两点中有一点到达自己的终点时,另一点也停止运动.设运动时间为
运动.当这两点中有一点到达自己的终点时,另一点也停止运动.设运动时间为 秒.
秒.
(1)请用
 表示点
表示点 的坐标为__________;
的坐标为__________;(2)是否存在某个时间
 ,使得以点
,使得以点 和四边形
和四边形 中的任意两个顶点为顶点的四边形为平行四边形?若存在,请求出
中的任意两个顶点为顶点的四边形为平行四边形?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励居民节约用电,我市自2012年以来对家庭用电收费实行阶梯电价,即每月对每户居民的用电量分为三个档级收费,第一档为用电量在180千瓦时(含180千瓦时)以内的部分,执行基本价格;第二档为用电量在180千瓦时到450千瓦时(含450千瓦时)的部分,实行提高电价;第三档为用电量超出450千瓦时的部分,执行市场调节价格. 我市一位同学家今年2月份用电330千瓦时,电费为213元,3月份用电240千瓦时,电费为150元.已知我市的一位居民今年4、5月份的家庭用电量分别为160和 410千瓦时,请你依据该同学家的缴费情况,计算这位居民4、5月份的电费分别为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为
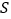 的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM=
的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM= EF,则正方形ABCD的面积为( )
EF,则正方形ABCD的面积为( )
A.
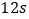 B.
B. 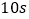 C.
C. 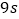 D.
D. 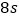
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD折叠,使点C与A点重合,折痕为EF.
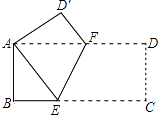
(1)判断四边形AFCE的形状,并说明理由.
(2)若AB=4,BC=8,求折痕EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在甲村至乙村的公路上有一块山地正在开发,现有一
 处需要爆破.已知点
处需要爆破.已知点 与公路上的停靠站
与公路上的停靠站 的距离为300米,与公路上的另一停靠站
的距离为300米,与公路上的另一停靠站 的距离为400米,且
的距离为400米,且 ,如图所示为了安全起见,爆破点
,如图所示为了安全起见,爆破点 周围半径250米范围内不得进入,问在进行爆破时,公路
周围半径250米范围内不得进入,问在进行爆破时,公路 段是否因为有危险而需要暂时封锁?请说明理由.
段是否因为有危险而需要暂时封锁?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以
 等为代表的战略性新兴产业.据统计,目前广东
等为代表的战略性新兴产业.据统计,目前广东 基站的数量约
基站的数量约 万座,计划到2020年底,全省
万座,计划到2020年底,全省 基站数量是目前的
基站数量是目前的 倍,到2022年底,全省
倍,到2022年底,全省 基站数量将达到
基站数量将达到 万座.
万座. 计划到2020年底,全省
计划到2020年底,全省 基站的数量是多少万座?
基站的数量是多少万座? 按照计划,求2020年底到2022年底,全省
按照计划,求2020年底到2022年底,全省 基站数量的年平均增长率;
基站数量的年平均增长率; 求2021年底全省
求2021年底全省 基站的数量.
基站的数量.
相关试题

