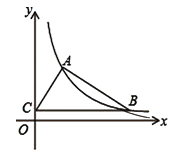
【题目】已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=![]()
求:(1)反比例函数的解析式;
(2)点C的坐标;
(3)∠ABC的余弦值.
参考答案:
【答案】(1)![]() ;(2)点C的坐标为(0,1);(3)
;(2)点C的坐标为(0,1);(3)![]() .
.
【解析】试题分析:(1)用待定系数法求解可得;(2)作AE⊥x轴于点E,AE与BC交于点F,则CF=2,根据tan∠ACB=![]() 得AF=3,即可知EF,从而得出答案;(3)先求出点B的坐标.继而由勾股定理得出AB的长,最后由三角函数可得答案.
得AF=3,即可知EF,从而得出答案;(3)先求出点B的坐标.继而由勾股定理得出AB的长,最后由三角函数可得答案.
试题解析:(1)设反比例函数解析式为y=![]() ,
,
将点A(2,4)代入,得:k=8,
∴反比例函数的解析式y=![]() ;
;
(2)过点A作AE⊥x轴于点E,AE与BC交于点F,则CF=2,
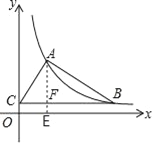
∵tan∠ACB=![]() ,
,
∴AF=3,
∴EF=1,
∴点C的坐标为(0,1);
(3)当y=1时,由1=![]() 可得x=8,
可得x=8,
∴点B的坐标为(1,8),
∴BF=BC﹣CF=6,
∴AB=![]()
∴cos∠ABC=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式①2x2﹣x,②(x﹣1)2﹣4(x﹣1)+4,③(x+1)2﹣4x(x+1)+4,④﹣4x2﹣1+4x;分解因式后,结果含有相同因式的是( )
A. ①④ B. ①② C. ③④ D. ②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C、D在坐标轴上,直线AB与直线CD:y=2x+2相交于点E(a,﹣3),连接BC,其中B(0,﹣5).
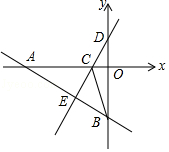
(1)求直线AB的解析式;
(2)求△BCE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如下图, AB∥CD , 点E , F分别为AB , CD上一点.
(1)在AB , CD之间有一点M(点M不在线段EF上),连接ME , MF , 试探究∠AEM , ∠EMF , ∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.
(2)如下图,在AB , CD之间有两点M , N , 连接ME , MN , NF , 请选择一个图形写出∠AEM , ∠EMN , ∠MNF , ∠NFC 存在的数量关系(不需证明).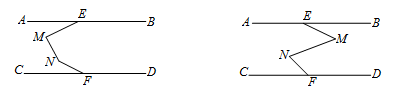
-
科目: 来源: 题型:
查看答案和解析>>【题目】一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作…若在第 n 次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.如图1,矩形ABCD中,若AB=2,BC=6,则称矩形ABCD为2阶奇异矩形.
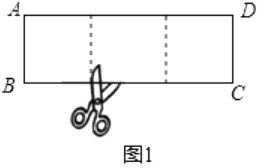
(1)判断与操作:
如图2,矩形ABCD的长为5,宽为2,它是奇异矩形吗?
如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.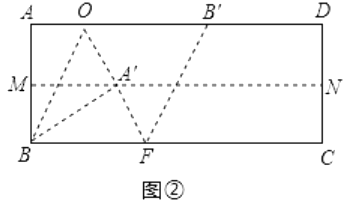
(2)探究与计算:
已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方写出a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
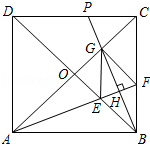
(1)求证:△OAE≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】化简3x2(﹣2x)的结果 .
相关试题

