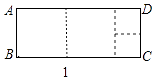
【题目】一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作…若在第 n 次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.如图1,矩形ABCD中,若AB=2,BC=6,则称矩形ABCD为2阶奇异矩形.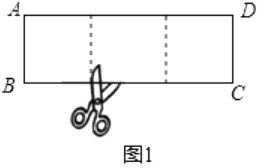
(1)判断与操作:
如图2,矩形ABCD的长为5,宽为2,它是奇异矩形吗?
如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.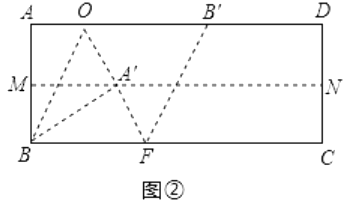
(2)探究与计算:
已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方写出a的值.
参考答案:
【答案】
(1)
解:判断与操作:
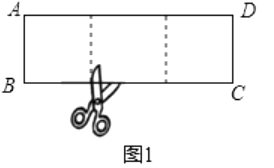
矩形ABCD是3阶奇异矩形,裁剪线的示意图如1所示:
(2)
解:探究与计算:
第一次操作后剩下的矩形的两边长度为a、(20﹣a),
第二次操作后剩下的矩形的两边长度为(20﹣2a)、a或(2a﹣20),(20﹣a),
∵矩形ABCD是3阶奇异矩形,
∴有①20﹣2a=2a,②a=2(20﹣2a),③20﹣a=2(2a﹣20),④2a﹣20=2(20﹣a),
解得:a1=5,a2=8,a3=12,a4=15.
裁剪线的示意图如2①、2②、2③、2④所示:
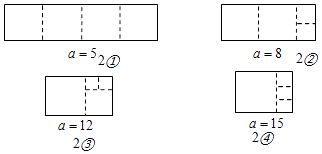
【解析】1、根据已知操作步骤画出即可;2、找出第一、二次操作后剩下矩形的两边长度,令其一边为另一边的二倍,解关于a的一元一次方程即可得出结论.
【考点精析】根据题目的已知条件,利用矩形的判定方法的相关知识可以得到问题的答案,需要掌握有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C、D在坐标轴上,直线AB与直线CD:y=2x+2相交于点E(a,﹣3),连接BC,其中B(0,﹣5).
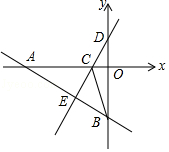
(1)求直线AB的解析式;
(2)求△BCE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如下图, AB∥CD , 点E , F分别为AB , CD上一点.
(1)在AB , CD之间有一点M(点M不在线段EF上),连接ME , MF , 试探究∠AEM , ∠EMF , ∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.
(2)如下图,在AB , CD之间有两点M , N , 连接ME , MN , NF , 请选择一个图形写出∠AEM , ∠EMN , ∠MNF , ∠NFC 存在的数量关系(不需证明).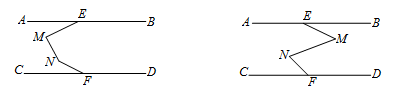
-
科目: 来源: 题型:
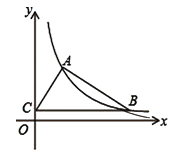
查看答案和解析>>【题目】已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=
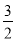
求:(1)反比例函数的解析式;
(2)点C的坐标;
(3)∠ABC的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
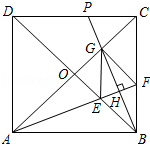
(1)求证:△OAE≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】化简3x2(﹣2x)的结果 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A.(x3)3=x6
B.﹣2x﹣3=﹣
C.3m2?2m4=6m8
D.a6÷a2=a4(a≠0)
相关试题

