【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
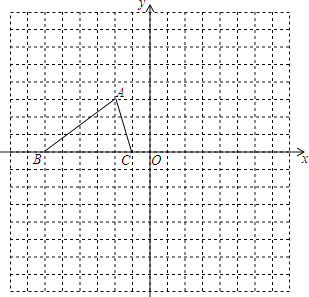
(1)将△ABC沿y轴翻折,则翻折后点A的对应点的坐标是 .
(2)作出△ABC关于x轴对称的图形△A1B1C1,画△A1B1C1,并直接写出点A1的坐标.
(3)若以D、B、C为顶点的三角形与△ABC全等,请画出所有符合条件的△DBC(点D与点A重合除外),并直接写出点D的坐标.
参考答案:
【答案】(1)(2,3);(2)(﹣2,﹣3);(3)(﹣2,﹣3)或(﹣5,3)或(﹣5,﹣3).
【解析】
试题分析:(1)直接利用关于y轴对称点的性质得出对应点位置;
(2)直接利用关于x轴对称点的性质得出对应点位置;
(3)直接利用全等三角形的判定方法得出对应点位置.
解:(1)翻折后点A的对应点的坐标是:(2,3);
故答案为:(2,3);
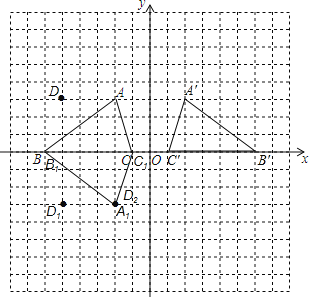
(2)如图所示:△A1B1C1,即为所求,A1(﹣2,﹣3);
(3)如图所示:D(﹣2,﹣3)或(﹣5,3)或(﹣5,﹣3).
-
科目: 来源: 题型:
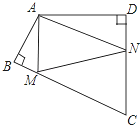
查看答案和解析>>【题目】如图,AB⊥BC,AD⊥DC,∠BAD=110°,在BC、CD上分别找一点M、N,当△AMN周长最小时,∠MAN的度数为 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在以AB为直径的半圆O上,延长BC到点D,使得CD=BC,过点D作DE⊥AB于点E,交AC于点F,点G为DF的中点,连接CG、OF、FB.
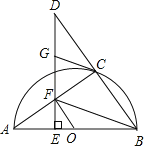
(1)求证:CG是⊙O的切线;
(2)若△AFB的面积是△DCG的面积的2倍,求证:OF∥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB.点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.

(1)若∠AEF=20°,∠ADE=50°,AC=2,求AB的长度;
(2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一副三角板的两个直角顶点重合在一起.
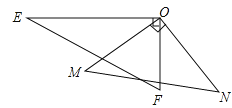
(1)若∠EON=140°,求∠MOF的度数;
(2)比较∠EOM与∠FON的大小,并写出理由;
(3)求∠EON+∠MOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=x2﹣1与x轴交点的个数( )
A.3 B.2 C.1 D.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=x2+bx+5配方后为y=(x﹣2)2+k,则b、k的值分别为( )
A. 0,5 B. 0,1 C. ﹣4,5 D. ﹣4,1
相关试题

