【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为_____.

参考答案:
【答案】![]() 或
或![]() .
.
【解析】如图1所示;点E与点C′重合时,
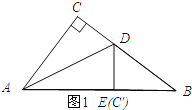
在Rt△ABC中,BC=![]() =4,
=4,
由翻折的性质可知;AE=AC=3、DC=DE,则EB=2,
设DC=ED=x,则BD=4-x,
在Rt△DBE中,DE2+BE2=DB2,即x2+22=(4-x)2,
解得:x=![]() ,
,
∴DE=![]() ;
;
如图2所示:∠EDB=90时,

由翻折的性质可知:AC=AC′,∠C=∠C′=90°,
∵∠C=∠C′=∠CDC′=90°,
∴四边形ACDC′为矩形,
又∵AC=AC′,
∴四边形ACDC′为正方形,
∴CD=AC=3,
∴DB=BC-DC=4-3=1,
∵DE∥AC,
∴△BDE∽△BCA,
∴![]() ,即
,即![]() ,
,
解得:DE=![]() ,
,
点D在CB上运动,∠DBC′<90°,故∠DBC′不可能为直角,
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式组
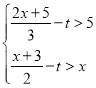 恰有三个整数解,则t的取值范围为__________.
恰有三个整数解,则t的取值范围为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】深圳市某校艺术节期间,开展了“好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布直方图(如图),请你根据图表提供的信息,解答下列问题:
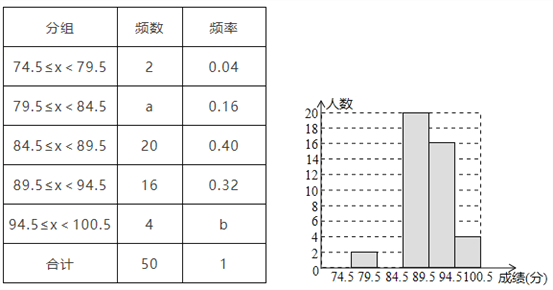
(1)频数、频率分布表中a=_______,b=_______;
(2)补全频数分布直方图;
(3)初赛成绩在94.5≤x<100.5分的四位同学恰好是七年级、八年级各一位,九年级两位,学生处打算从中随机挑选两位同学谈一下决赛前的训练,则所选两位同学恰好都是九年级学生的概率为_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解社区居民最喜欢的支付方式,某兴趣小组对龙湖社区内20~60岁年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
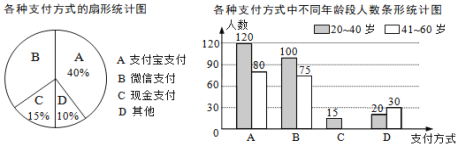
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中20~60岁的居民约4000人,估算这些人中最喜欢微信支付方式的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】认真阅读下面的材料,完成有关问题.
材料:在学习绝对值时,老师教过我们绝对值的几何含义,一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为|a﹣b|.
问题(1):点A、B、C在数轴上分别表示有理数x、﹣2、1,那么A到B的距离与A到C的距离之和可表示为 (用含绝对值的式子表示).
问题(2):利用数轴探究:①找出满足|x﹣3|+|x+1|=6的x的所有值是 ;
②设|x﹣3|+|x+1|=p,当x的值取在不小于﹣1且不大于3的范围时,p的值是不变的,而且是p的最小值,这个最小值是 ;当x的值取在 的范围时,|x|+|x﹣2|的最小值是 .
问题(3):求|x﹣3|+|x﹣2|+|x+1|的最小值以及此时x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着科技的发展,某快递公司为了提高分拣包裹的速度,使用机器人代替人工进行包裹分拣,若甲机器人工作
 ,乙机器人工作
,乙机器人工作 ,一共可以分拣700件包裹;若甲机器人工作
,一共可以分拣700件包裹;若甲机器人工作 ,乙机器人工作
,乙机器人工作 ,一共可以分拣650件包裹.
,一共可以分拣650件包裹.(1)求甲、乙两机器人每小时各分拣多少件包裹;
(2)去年“双十一”期间,快递公司的业务量猛增,为了让甲、乙两机器人每天分拣包裹的总数量不低于2250件,则它们每天至少要一起工作多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地计划用120~180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米3.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式.并给出自变量x的取值范围;
(2)由于工程进度的需要,实际平均每天运送土石方比原计划多20%,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少万米3?
相关试题

