【题目】认真阅读下面的材料,完成有关问题.
材料:在学习绝对值时,老师教过我们绝对值的几何含义,一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为|a﹣b|.
问题(1):点A、B、C在数轴上分别表示有理数x、﹣2、1,那么A到B的距离与A到C的距离之和可表示为 (用含绝对值的式子表示).
问题(2):利用数轴探究:①找出满足|x﹣3|+|x+1|=6的x的所有值是 ;
②设|x﹣3|+|x+1|=p,当x的值取在不小于﹣1且不大于3的范围时,p的值是不变的,而且是p的最小值,这个最小值是 ;当x的值取在 的范围时,|x|+|x﹣2|的最小值是 .
问题(3):求|x﹣3|+|x﹣2|+|x+1|的最小值以及此时x的值.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() 和4;②4;当x的取值在不小于0且不大于2的范围时,
和4;②4;当x的取值在不小于0且不大于2的范围时,![]() 的最小值是2;(3)
的最小值是2;(3)![]() 的最小值为4,此时x的值为2.
的最小值为4,此时x的值为2.
【解析】
(1)根据材料中两点间距离的表示方法,分别表示出A到B的距离、A到C的距离,然后求和即可;
(2)①![]() 表示的是在数轴上的一点到
表示的是在数轴上的一点到![]() 的距离之和为6,因此分三种情况分析,去绝对值计算即可;
的距离之和为6,因此分三种情况分析,去绝对值计算即可;
②先根据x的取值范围去绝对值,再求解即可得出答案;利用同样的方法,分析![]() 即可;
即可;
(3)根据数轴的定义,划分x的取值范围,去绝对值进行计算即可.
(1)由题意得:A到B的距离为![]() ,A到C的距离为
,A到C的距离为![]()
则所求的式子为:![]() ;
;
(2)①![]() 表示的是在数轴上的一点到
表示的是在数轴上的一点到![]() 的距离之和为6
的距离之和为6
分以下三种情况:
当![]() 时,
时,![]() 可化为
可化为![]() ,解得
,解得![]()
当![]() 时,
时,![]() 可化为
可化为![]() ,无解,不满足题意
,无解,不满足题意
当![]() 时,
时,![]() 可化为
可化为![]() ,解得
,解得![]()
综上,满足![]() 的x的所有值是
的x的所有值是![]() 和4;
和4;
②由题意得,当![]() 时,p取得最小值
时,p取得最小值
![]()
则p的最小值是4
![]() 表示的是在数轴上的一点到
表示的是在数轴上的一点到![]() 的距离之和
的距离之和
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
综上,当x的取值在不小于0且不大于2的范围时,![]() 的最小值是2;
的最小值是2;
(3)![]() 表示的是在数轴上的一点到
表示的是在数轴上的一点到![]() 的距离之和
的距离之和
当![]() 时,
时,![]()
当![]() 时,
时,![]()
此时,![]() ,则
,则![]()
当![]() 时,
时,![]()
此时,![]()
当![]() 时,
时,![]()
综上,![]() 的最小值为4,此时
的最小值为4,此时![]() ,解得
,解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】深圳市某校艺术节期间,开展了“好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布直方图(如图),请你根据图表提供的信息,解答下列问题:
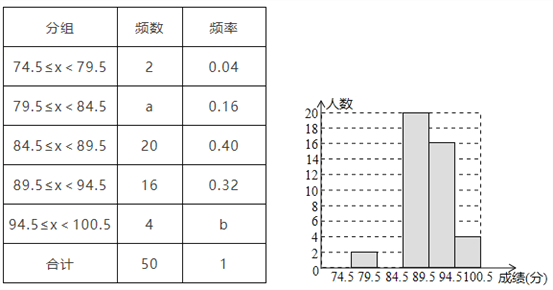
(1)频数、频率分布表中a=_______,b=_______;
(2)补全频数分布直方图;
(3)初赛成绩在94.5≤x<100.5分的四位同学恰好是七年级、八年级各一位,九年级两位,学生处打算从中随机挑选两位同学谈一下决赛前的训练,则所选两位同学恰好都是九年级学生的概率为_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解社区居民最喜欢的支付方式,某兴趣小组对龙湖社区内20~60岁年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
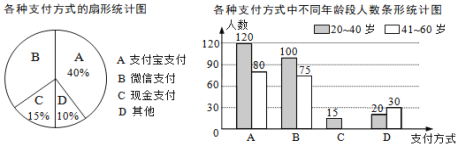
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中20~60岁的居民约4000人,估算这些人中最喜欢微信支付方式的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着科技的发展,某快递公司为了提高分拣包裹的速度,使用机器人代替人工进行包裹分拣,若甲机器人工作
 ,乙机器人工作
,乙机器人工作 ,一共可以分拣700件包裹;若甲机器人工作
,一共可以分拣700件包裹;若甲机器人工作 ,乙机器人工作
,乙机器人工作 ,一共可以分拣650件包裹.
,一共可以分拣650件包裹.(1)求甲、乙两机器人每小时各分拣多少件包裹;
(2)去年“双十一”期间,快递公司的业务量猛增,为了让甲、乙两机器人每天分拣包裹的总数量不低于2250件,则它们每天至少要一起工作多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地计划用120~180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米3.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式.并给出自变量x的取值范围;
(2)由于工程进度的需要,实际平均每天运送土石方比原计划多20%,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少万米3?
-
科目: 来源: 题型:
查看答案和解析>>【题目】从谢家集到田家庵有3路,121路,26路三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从谢家集到田家庵的用时时间,在每条线路上随机选取了450个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:早高峰期间,乘坐______(填“3路”,“121路”或“26路”)线路上的公交车,从谢家集到田家庵“用时不超过50分钟”的可能性最大.
用时



合计(频次)
线路
3路
260
167
23
450
121路
160
166
124
450
26路
50
122
278
450
相关试题

