【题目】已知关于x的不等式组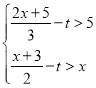 恰有三个整数解,则t的取值范围为__________.
恰有三个整数解,则t的取值范围为__________.
参考答案:
【答案】![]()
【解析】
先求出不等式组的解集,再根据不等式组恰有三个整数解,结合数轴,分4种情况分析讨论,分别求解即可.

解不等式①得:![]()
解不等式②得:![]()
要使不等式组有解,则![]() ,解得:
,解得:![]()
此时,![]()
则不等式组的解集为:![]()
要使不等式组恰有三个整数解,需分以下4种情况讨论:
(1)当不等式组的解集表示在数轴上如图1时,其恰好有2,3,4三个整数解
则 ,解得:
,解得: ,无公共部分,不符合题意
,无公共部分,不符合题意

(2)当不等式组的解集表示在数轴上如图2时,其恰好有3,4,5三个整数解
则 ,解得:
,解得: ,公共部分为
,公共部分为![]()

(3)当不等式组的解集表示在数轴上如图3时,其恰好有4,5,6三个整数解
则 ,解得:
,解得: ,无公共部分,不符合题意
,无公共部分,不符合题意

(4)当不等式组的解集表示在数轴上如图4时,其恰好有5,6,7三个整数解
则 ,解得:
,解得: ,无公共部分,不符合题意
,无公共部分,不符合题意

综上,当![]() 时,题干中的不等式组恰好有三个整数解
时,题干中的不等式组恰好有三个整数解
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC中,AB∥OC,边OA在x轴的正半轴上,OC在y轴的正半轴上,点B在第一象限内,点D为AB的中点,CD与OB相交于点E,若△BDE、△OCE的面积分别为1和9,反比例函数y=
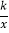 的图象经过点B,则k=_______.
的图象经过点B,则k=_______.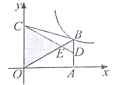
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,等腰直角三角形AOB的直角顶点A在第四象限,顶点B(0,-2),点C(0,1),点D在边AB上,连接CD交OA于点E,反比例函数
 的图像经过点D,若△ADE和△OCE的面积相等,则k的值为___________.
的图像经过点D,若△ADE和△OCE的面积相等,则k的值为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生每周课外阅读时间的情况,对3000名学生采用随机抽样的方式进行了问卷调查,调查结果分为“2小时以内”、“2小时~3小时”、“3小时~4小时”和“4小时以上”四个等级,分别用A、B、C、D表示,根据调查结果绘制成了如图所示的两幅不完整的统计图,由图中所给出的信息解答下列问题:

(1)x= ,样本容量是 ;
(2)将不完整的条形统计图补充完整;
(3)请估计该校3000名学生中每周课外阅读时间在“2小时以上”的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】深圳市某校艺术节期间,开展了“好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布直方图(如图),请你根据图表提供的信息,解答下列问题:
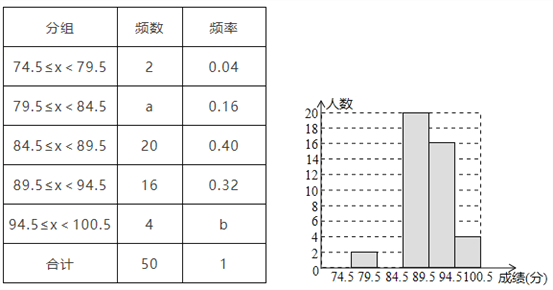
(1)频数、频率分布表中a=_______,b=_______;
(2)补全频数分布直方图;
(3)初赛成绩在94.5≤x<100.5分的四位同学恰好是七年级、八年级各一位,九年级两位,学生处打算从中随机挑选两位同学谈一下决赛前的训练,则所选两位同学恰好都是九年级学生的概率为_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解社区居民最喜欢的支付方式,某兴趣小组对龙湖社区内20~60岁年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
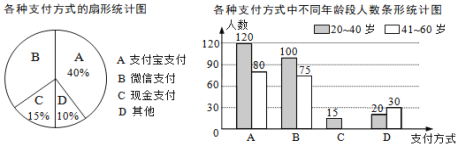
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中20~60岁的居民约4000人,估算这些人中最喜欢微信支付方式的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为_____.

相关试题

