【题目】已知![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,则
,则![]() 的度数为( )
的度数为( )
A.![]() B.15°或
B.15°或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
参考答案:
【答案】A
【解析】
根据题意画出图形,分两种情况讨论:∠BOC在∠AOB内部和外部;当∠BOC在∠AOB内部时,根据角平分线的定义以及角的和差可得∠MON=∠AOM∠AON,当∠BOC在∠AOB外部时可得∠MON=∠AON-∠AOM.
解:如图所示,当∠BOC在∠AOB内部时,
∵∠AOB=80°,其角平分线为OM,
∴∠AOM=40°,
∵∠BOC=30°,
∴∠AOC=50°,
∵![]() 平分
平分![]() ,
,
∴∠AON=25°,
∴∠MON=∠AOM∠AON=40°25°=15°;
如图所示,当∠BOC在∠AOB外部时,

∵∠AOB=80°,其角平分线为OM,
∴∠AOM=40°,
∵∠BOC=30°,
∴∠AOC=110°,
∵![]() 平分
平分![]() ,
,
∴∠AON=55°,
∴∠MON=∠AON-∠AOM=55°-40°=15°.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式A=x2+xy+2y-
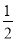 ,B=2x2-2xy+x-1.
,B=2x2-2xy+x-1.(1)求2A-B;
(2)当x=-1,y=-2时,求2A-B的值;
(3)若2A-B的值与x的取值无关,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”的方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是 (请直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售A、B两种品牌的洗衣机,进价及售价如下表:
(1)该商场9月份用45000元购进A、B两种品牌的洗衣机,全部售完后获利9600元,求商场9月份购进A、B两种洗衣机的数量;

(2)该商场10月份又购进A、B两种品牌的洗衣机共用去36000元,
①问该商场共有几种进货方案?请你把所有方案列出来.
②通过计算说明洗衣机全部销售完后哪种进货方案所获得的利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A,B,C,D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2-2x-3,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为____.
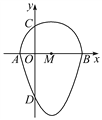
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加x元.求:
(1)房间每天的入住量y(间)关于x(元)的函数关系式;
(2)该宾馆每天的房间收费z(元)关于x(元)的函数关系式;
(3)该宾馆客房部每天的利润w(元)关于x(元)的函数关系式;当每个房间的定价为每天多少元时,w有最大值?最大值是多少?
相关试题

