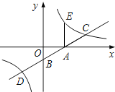
【题目】如图,直线![]() 与
与![]() ,
,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与反比例函数
,与反比例函数![]() 图象交于点
图象交于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴的垂线交该反比例函数图象于点
轴的垂线交该反比例函数图象于点![]() .
.
![]() 求点
求点![]() 的坐标.
的坐标.
![]() 若
若![]() .
.
①求![]() 的值.
的值.
②试判断点![]() 与点
与点![]() 是否关于原点
是否关于原点![]() 成中心对称?并说明理由.
成中心对称?并说明理由.
参考答案:
【答案】![]() 点
点![]() 的坐标为
的坐标为![]() ;②点
;②点![]() 与点
与点![]() 关于原点
关于原点![]() 成中心对称.理由见解析.
成中心对称.理由见解析.
【解析】
(1)令一次函数中y=0,解关于x的一元一次方程,即可得出结论;
(2)①过点C作CF⊥x轴于点F,设AE=AC=t,由此表示出点E的坐标,利用特殊角的三角形函数值,通过计算可得出点C的坐标,再根据反比例函数图象上点的坐标特征可得出关于t的一元二次方程,解方程即可得出结论;
②根据点在直线上设出点D的坐标,根据反比例函数图象上点的坐标特征可得出关于点D横坐标的一元二次方程,解方程即可得出点D的坐标,结合①中点E的坐标即可得出结论.
![]() 当
当![]() 时,得
时,得![]() ,解得:
,解得:![]() .
.
∴点![]() 的坐标为
的坐标为![]() .:
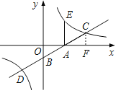
.:![]() ①过点
①过点![]() 作
作![]() 轴于点
轴于点![]() ,如图所示.
,如图所示.
设![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,
B(0,![]() )∴AB=3
)∴AB=3
∵![]()
∴![]()
∴![]() ,
,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() .
.
∴![]() ,
,
解得:![]() (舍去),
(舍去),![]() .
.
∴![]() .
.
②点![]() 与点
与点![]() 关于原点
关于原点![]() 成中心对称,理由如下:
成中心对称,理由如下:
设点![]() 的坐标是
的坐标是![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() .
.
又∵点![]() 的坐标为
的坐标为![]() ,
,
∴点![]() 与点
与点![]() 关于原点
关于原点![]() 成中心对称.
成中心对称.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 与
与 交于A,B两点,且点A的横坐标为4,过原点O的另一条直线l交双曲线
交于A,B两点,且点A的横坐标为4,过原点O的另一条直线l交双曲线 于P,Q两点(点P在第一象限),由点A,B,P,Q为顶点组成的四边形面积为24,则点P的坐标为_________.
于P,Q两点(点P在第一象限),由点A,B,P,Q为顶点组成的四边形面积为24,则点P的坐标为_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】等边三角形ABC 中,BD是角平分线,点E在BC边的延长线上,且CD=CE,则∠BDE的度数是( )
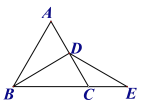
A.90°B.100°C.120°D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
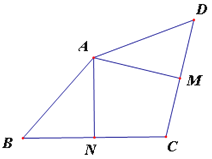
查看答案和解析>>【题目】如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC。
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数
 的图象过点
的图象过点 .
. 求该函数的解析式;
求该函数的解析式; 过点
过点 分别向
分别向 轴和
轴和 轴作垂线,垂足为
轴作垂线,垂足为 和
和 ,求四边形
,求四边形 的面积;
的面积; 求证:过此函数图象上任意一点分别向
求证:过此函数图象上任意一点分别向 轴和
轴和 轴作垂线,这两条垂线与两坐标轴所围成矩形的面积为定值.
轴作垂线,这两条垂线与两坐标轴所围成矩形的面积为定值.
相关试题

