【题目】在正方形ABCD中,
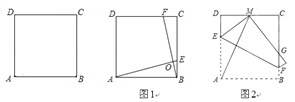
(1)如图1,若点E,F分别在边BC,CD上,AE,BF交于点O,且∠AOF=90°.求证:AE =BF.
(2)如图2,将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.若DC=5,CM=2,求EF的长.
参考答案:
【答案】(1)证明见解析;(2) ![]() .
.
【解析】(1) 分析:(1)根据矩形的对边平行且相等得到AB=BC,∠DCB=∠ABE.再结合一对直角相等即可证明三角形全等;(2) 由折叠的性质得全等三角形的对应边相等以及勾股定理,可以求得DF,EF的长;再根据勾股定理求得DE的长,运用三角函数定义求解.
本题解析:
(1)证明:∵四边形ABCD是正方形,∴AB=BC,
∠ABE=∠BCF=90°,∵∠AOF=90°,∠AOB=90°,
∴∠BAE+∠OBA=90°,又∵∠FBC+∠OBA=90°,
∴∠BAE=∠CBF(同角的余角相等),在△ABE和△BCF中
∴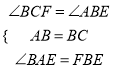
∴△ABE≌△BCF(ASA).∴AE=BF.
(2) 作MG⊥AB于G,作FH⊥AD于H,如图所示:
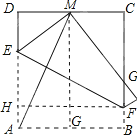
则MG=AD,FH=AB,∴MG=FH,
在△AMG和△EFH中, 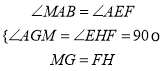 ,
,
∴△AMG≌△EFH(AAS),∴AM=EF;∵DC=AD=5,CM=2,∴DM=5-2=3
在Rt△ADM中,根据勾股定理得:AM=![]() ,
,
∴EF=AM=![]() .
.
-
科目: 来源: 题型:
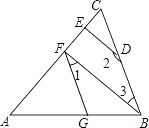
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,连结CD,延长AC,BD,相交于点F.现给出下列结论:
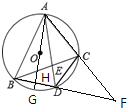
①若AD=5,BD=2,则DE=
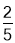 ;
;②
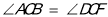 ;
;③
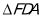 ∽
∽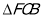 ;
;④若直径AG⊥BD交BD于点H,AC=FC=4,DF=3,则cosF=
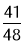 ;
;则正确的结论是( )
A.①③ B.②③④ C.③④ D.①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列算式:
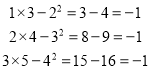
…….
(1)请你按以上规律写出第4个算式:_________________________
(2)把这个规律用含字母的式子表示出来____________________
(3)你认为(2)中所写的式子一定成立吗?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程是一元二次方程的一般形式的是( )
A.(x-1)2=16B.3(x-2)2=27C.5x2-3x=0D.x2+2x=8
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程mx2+(m-1)x-10=0有一个根为2,则m的值是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,平行四边形ABCD的周长为20cm,且AD-AB=2cm,则AD=_________cm
相关试题

