【题目】如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,连结CD,延长AC,BD,相交于点F.现给出下列结论:
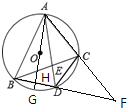
①若AD=5,BD=2,则DE=![]() ;
;
②![]() ;
;
③![]() ∽
∽![]() ;
;
④若直径AG⊥BD交BD于点H,AC=FC=4,DF=3,则cosF=![]() ;
;
则正确的结论是( )
A.①③ B.②③④ C.③④ D.①②④
参考答案:
【答案】C
【解析】
试题分析:此题主要考查圆的综合问题,熟悉圆的相关性质,会证明三角形相似并解决相关问题,能灵活运用垂径定理和三角函数是解题的关键.
①只需证明△BDE∽△ADB,运用对应线段成比例求解即可; ②连接CD,假设∠ACB=∠DCF,推出与题意不符即可判断; ③由公共角和同弧所对的圆周角相等即可判断; ④先证明△FCD∽△FBA,求出BD的长度,根据垂径定理求出DH,结合三角函数即可求解.
①如图1,∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠CAD=∠CBD,
∴∠BAD=∠CBD,
∵∠BDE=∠BDE,
∴△BDE∽△ADB,
∴![]() ,
,
由AD=5,BD=2,可求DE=![]() ,
,
①不正确;
②如图2,
连接CD,
∠FCD+∠ACD=180°,∠ACD+∠ABD=180°,
∴∠FCD=∠ABD,
若∠ACB=∠DCF,因为∠ACB=∠ADB,
则有:∠ABD=∠ADB,与已知不符,
故②不正确;
③如图3,
∵∠F=∠F,∠FAD=∠FBC,
∴△FDA∽△FCB;
故③正确;
④如图4,连接CD,由②知:∠FCD=∠ABD,
又∵∠F=∠F,
∴△FCD∽△FBA,
∴![]() ,
,
由AC=FC=4,DF=3,可求:AF=8,FB=![]() ,
,
∴BD=BF-DF=![]() ,
,
∵直径AG⊥BD,
∴DH=![]() ,
,
∴FG=![]() ,
,
∴cosF=![]() =
=![]() ,
,
故④正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程2x(x﹣1)=12+x(2x﹣5)的解是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算错误的是( )
A.(a2)3(﹣a3)2=a12
B.(﹣ab2)2(﹣a2b3)=a4b7
C.(2xyn)(﹣3xny)2=18x2n+1yn+2
D.(﹣xy2)(﹣yz2)(﹣zx2)=﹣x3y3z3 -
科目: 来源: 题型:
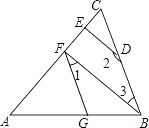
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列算式:
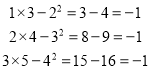
…….
(1)请你按以上规律写出第4个算式:_________________________
(2)把这个规律用含字母的式子表示出来____________________
(3)你认为(2)中所写的式子一定成立吗?并说明理由.
-
科目: 来源: 题型:
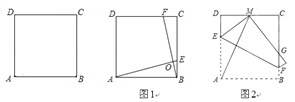
查看答案和解析>>【题目】在正方形ABCD中,
(1)如图1,若点E,F分别在边BC,CD上,AE,BF交于点O,且∠AOF=90°.求证:AE =BF.
(2)如图2,将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.若DC=5,CM=2,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程是一元二次方程的一般形式的是( )
A.(x-1)2=16B.3(x-2)2=27C.5x2-3x=0D.x2+2x=8
相关试题

