【题目】已知直线![]() .
.
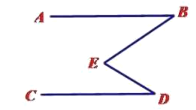
(1)如下图,点![]() 在直线
在直线![]() 的左侧,请写出
的左侧,请写出![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由:
之间的数量关系,并说明理由:
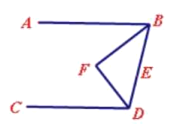
(2)如下图,当点![]() 在线段
在线段![]() 上时,
上时,![]() 分别平分
分别平分![]() ,
,![]() ,此时
,此时![]() 的度数为_________°
的度数为_________°
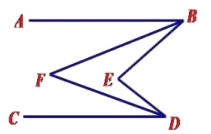
(3)如下图,当点![]() 在直线
在直线![]() 的左侧时,
的左侧时,![]() 分别平分
分别平分![]() ,
,![]() ,请直接写出
,请直接写出![]() 和
和![]() 的数量关系 ;
的数量关系 ;
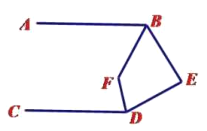
(4)如下图,当点![]() 在直线
在直线![]() 的右侧时,
的右侧时,![]() 分别平分
分别平分![]() ,
,![]() ,请直接写出
,请直接写出![]() 和
和![]() 的数量关系 ;
的数量关系 ;
参考答案:
【答案】(1)∠ABE+∠CDE=∠BED,理由见解析;(2)90;(3)∠BFD=![]() ∠BED;(4)2∠BFD+∠BED=360°
∠BED;(4)2∠BFD+∠BED=360°
【解析】
(1)首先作EF∥AB,根据直线AB∥CD,可得EF∥CD,所以∠ABE=∠1,∠CDE=∠2,据此推得∠ABE+∠CDE=∠BED即可.
(2)作GF∥AB,根据∠ABD+∠CDB=180°,![]() 分别平分
分别平分![]() ,
,![]() ,得到∠BFD=∠BFG+∠DFG=∠ABF+∠CDF=
,得到∠BFD=∠BFG+∠DFG=∠ABF+∠CDF=![]() (∠ABD+∠CDB)=90°;
(∠ABD+∠CDB)=90°;
(3)首先根据BF,DF分别平分∠ABE,∠CDE,推得∠ABF+∠CDF=![]() (∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CDF,∠BED=∠ABE+∠CDE,据此推得∠BFD=
(∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CDF,∠BED=∠ABE+∠CDE,据此推得∠BFD=![]() ∠BED.
∠BED.
(4)首先过点E作EG∥CD,再根据AB∥CD,EG∥CD,推得AB∥CD∥EG,所以∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,据此推得∠ABE+∠CDE+∠BED=360°;然后根据∠BFD=∠ABF+∠CDF,以及BF,DF分别平分∠ABE,∠CDE,推得2∠BFD+∠BED=360°即可.
(1)∠ABE+∠CDE=∠BED.
理由:如图1,作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠ABE=∠1,∠CDE=∠2,
∴∠ABE+∠CDE=∠1+∠2=∠BED,
即∠ABE+∠CDE=∠BED.
故答案为:∠ABE+∠CDE=∠BED;
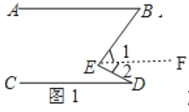
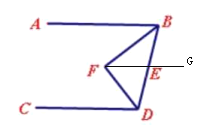
(2)如图,作GF∥AB,
∴AB∥GF∥CD
∴∠ABD+∠CDB=180°,∠BFG=∠ABF,∠DFG=∠CDF
∵![]() 分别平分
分别平分![]() ,
,![]() ,
,
∴∠BFD=∠BFG+∠DFG=∠ABF+∠CDF=![]() ∠ABD +
∠ABD +![]() ∠CDB =
∠CDB =![]() (∠ABD+∠CDB)=90°,
(∠ABD+∠CDB)=90°,
故答案为:90;
(3)∠BFD=![]() ∠BED.
∠BED.
理由:如图
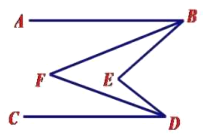
∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠ABF+∠CDF=![]() ∠ABE+
∠ABE+![]() ∠CDE=
∠CDE=![]() (∠ABE+∠CDE),
(∠ABE+∠CDE),
由(1)可得∠BFD=∠ABF+∠CDF=![]() (∠ABE+∠CDE)
(∠ABE+∠CDE)
又∠BED=∠ABE+∠CDE,
∴∠BFD=![]() ∠BED.
∠BED.
(4)2∠BFD+∠BED=360°.
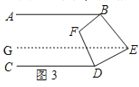
理由:如图3,过点E作EG∥CD,
∵AB∥CD,EG∥CD,
∴AB∥CD∥EG,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠CDE+∠BED=360°,
由(1)知,∠BFD=∠ABF+∠CDF,
又∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠BFD=![]() (∠ABE+∠CDE),
(∠ABE+∠CDE),
∴2∠BFD+∠BED=360°.
故答案为:2∠BFD+∠BED=360°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求△ABC的周长和面积.

-
科目: 来源: 题型:
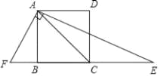
查看答案和解析>>【题目】如图,正方形ABCD边长为1,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CE于点F,则EF的长为____.
-
科目: 来源: 题型:
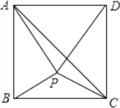
查看答案和解析>>【题目】如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
求证:(1)△APB≌△DPC;(2)∠BAP=2∠PAC.
-
科目: 来源: 题型:
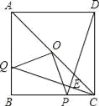
查看答案和解析>>【题目】如图,AC是正方形ABCD的对角线,点O是AC的中点,点Q是AB上一点,连接CQ,DP⊥CQ于点E,交BC于点P,连接OP,OQ;
求证:(1)△BCQ≌△CDP;(2)OP=OQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为2a ,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形.
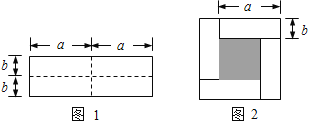
(1)图2的阴影部分的正方形的边长是 ______.
(2)用两种不同的方法求图中阴影部分的面积.
(方法1)
 = _____________;
= _____________; (方法2)
 =______________;
=______________;(3)观察如图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.

相关试题

